3.1: The Laws of Thermodynamics

Two fundamental concepts govern energy as it relates to living organisms: the First Law of Thermodynamics states that total energy in a closed system is neither lost nor gained — it is only transformed. The Second Law of Thermodynamics states that entropy constantly increases in a closed system.

More specifically, the First Law states that energy can neither be created nor destroyed: it can only change form. Therefore, through any and all processes, the total energy of the universe or any other closed system is constant. In a simple thermodynamic system, this means that the energy is transformed either by the transfer of heat energy (i.e. heating and cooling of a substance) or by the production of mechanical work (i.e. movement). In biological and chemical terms, this idea can be extended to other forms of energy such as the chemical energy stored in the bonds between atoms of a molecule, or the light energy that can be absorbed by plant leaves.

Work, in this case, need not imply a complicated mechanism. In fact, there is work accomplished by each molecule in the simple expansion of a heated mass of gaseous molecules (as visualized by expansion of a heated balloon, for example). This is expressed mathematically as the Fundamental Thermodynamic Relation:

in which \(E\) is internal energy of the system, \(T\) is temperature, \(S\) is entropy, \(p\) is pressure, and \(V\) is volume.

Unlike the First Law which applies even to particles within a system, the Second Law is a statistical law — it applies generally to macroscopic systems. However, it does not preclude smallscale variations in the direction of entropy over time. In fact, the Fluctuation theorem (proposed in 1993 by Evans et al, and demonstrated by Wang et al in 2002) states that as the length of time or the system size increases, the probability of a negative change in entropy (i.e. going against the Second Law) decreases exponentially. So on very small time scales, there is a real probability that fluctuations of entropy against the Second Law can exist.

The Second Law dictates that entropy always seeks to increase over time. Entropy is simply a fancy word for chaos or disorder. The theoretical final or equilibrium state is one in which entropy is maximized, and there is no order to anything in the universe or closed system. Spontaneous processes, those that occur without external influence, are always processes that convert order to disorder. However, this does not preclude the imposition of order upon a system. Examining the standard mathematical form of the Second Law:

ΔS_system + ΔS_surroundings = ΔS_universe,

where ΔS_universe > 0

shows that entropy can decrease within a system as long as there is an increase of equal or greater magnitude in the entropy of the surroundings of the system.

The phrase “in a closed system” is a key component of these laws, and it is with the idea encapsulated in that phrase that life can be possible. Let’s think about a typical cell: in its lifetime, it builds countless complex molecules - huge proteins and nucleic acids formed from a mixture of small amino acids or nucleotides, respectively. On its surface, this example might seem to be a counterexample to the second law - clearly going from a mixture of various small molecules to a larger molecule with bonded and ordered components would seem to be a decrease in entropy (or an increase in order). How is this possible with respect to the second law? It is, because the second law applies only to closed systems. That is, a system that neither gains nor loses matter or energy.

The “universe” is a closed system by definition because there is nothing outside of it.

A living cell is not a closed system: it has inputs and outputs. However, the second law is still useful if we recognize that the only way that it can be bypassed is through the input of energy. If a cell cannot take in food (input of matter and energy into the system) it dies, because the second law requires that everything eventually breaks down into more random/chaotic collections of smaller components. The order required to sustain life (think about all the different complex molecules that were mentioned in the previous chapter) is phenomenal. The same thing applies on the organismal level (Figure \(\PageIndex{1}\)) - without an input of energy (in the form of food molecules for animals or in the form of light for plants), the organism will die and subsequently decompose.

Figure \(\PageIndex{1}\). In the top panel, depicting an open system in which there are inputs for matter and energy (in the form of food), the box is open and air can be exchanged, food dropped in, etc, thus allowing the mouse to grow. However, in the bottom panel, depicting a closed system, the mouse does not have ready access any more oxygen than is in the box, nor does it have access to food. Without these inputs, the second law takes effect, and the mouse dies and decomposes into many smaller molecules.

Creating molecules from atoms costs energy because it takes a disordered collection of atoms and forces them, through chemical bonds, into ordered, non-random positions. There is likewise an energy cost to formation of macromolecules from smaller molecules. By imposing order in the system, there must be an associated input of energy. This happens at every level of the system: atoms to molecules, small molecules to macromolecules, groups of molecules to organelles, etc.

As the polymerizing reaction reduces entropy, it requires energy generated (usually) by the breakdown of ATP into AMP and PPi, which is a reaction that increases entropy.

Where does that energy go? It ends up in the bonds that are holding the molecules or macromolecules in their ordered state. When such a bond is broken, and a molecule is turned back into a collection of atoms, energy is released. The energy in a chemical bond is thus potential energy - it is stored energy that, when released, has the ability to do work. This term, if you recall your high school physics, is usually learned along with kinetic energy, which is energy that is being used in the process of actually doing work (i.e. moving an object from one place to another). The classic example is the rock on the top of a hill: it has potential energy because it is elevated and could potentially come down. As it tumbles down, it has kinetic energy as it moves. Similarly in a cell, the potential energy in a chemical bond can be released and then used for processes such as putting smaller molecules together into larger molecules, or causing a molecular motor to spin or bend - actions that could lead to pumping of protons or the contraction of muscle cells, respectively.

Coming back to the second law, it essentially mandates that breaking down molecules releases energy and that making new molecules (going against the natural tendency towards disorder) requires energy. Every molecule has an intrinsic energy, and therefore whenever a molecule is involved in a chemical reaction, there will be a change in the energy of the resulting molecule(s). Some of this change in the energy of the system will be usable to do work, and that energy is referred to as the free energy of the reaction. The remainder is given off as heat.

The Gibbs equation describes this relationship as

\[ΔG= ΔH-TΔS \]

where ΔG is the change in free energy, ΔH is the change in enthalpy (roughly equivalent to heat), T is the temperature at which the reaction takes place, and ΔS is the change in entropy. As a matter of convention, release of free energy is a negative number, while a requirement for input of energy is denoted with a positive number. Generally, a chemical reaction in which ΔG < 0 is a spontaneous reaction (also called an exergonic reaction), while a chemical reaction in which ΔG > 0 is not spontaneous (or endergonic). When ΔG = 0, the system is in equilibrium. ΔG can also be expressed with respect to the concentration of products and reactants:

\[ΔG = ΔG^o + RT \ln \left( \dfrac{[P_1][P_2][P_3]...}{[R_1][R_2][R_3]...}\right)\]

Terms in square brackets denote concentrations, ΔG° is the standard free energy for the reaction (as carried out with 1M concentration of each reactant, at 298K and at 1 atm pressure), R is the gas constant (1.985 cal K^-1mol^-1), and T is the temperature in Kelvin. In a simpler system in which there are just two reactants and two products:

\[\ce{aA + bB <=> cC + dD}\]

the equation for free energy change becomes

ΔG = ΔG° + RTln([C]^c[D]^d/[A]^a[B]^b)

This is important to us as cell biologists because although cells are not very well suited to regulating chemical reactions by varying the temperature or the pressure of the reaction conditions, they can relatively easily alter the concentrations of substrates and products. In fact, by doing so, it is even possible to drive a non-spontaneous reaction (ΔG > 0) forward spontaneously (ΔG < 0) either by increasing substrate concentration (possibly by transporting them into the cell) or by decreasing product concentration (either secreting them from the cell or by using them up as substrates for a different chemical reaction).

Changes in substrate or product concentration to drive a non-spontaneous reaction are an example of the more general idea of coupling reactions to drive an energetically unfavorable reactions forward. Endergonic reactions can be coupled to exergonic reactions as a series of reactions that ultimately is able to proceed forward. The only requirement is that the overall free energy change must be negative (ΔG < 0). So, assuming standard conditions (ΔG = ΔG°’), if we have a reaction with a free energy change of +5 kcal/mol, it is non-spontaneous. However, if we couple this reaction, to ATP hydrolysis for example, then both reactions will proceed because the standard free energy change of ATP hydrolysis to ADP and phosphate is an exergonic -7.3 kcal/mol. The sum of the two ΔG values is -2.3 kcal/mol, which means the coupled series of reactions is spontaneous.

In fact, ATP is the most common energy “currency” in cells precisely because the -7.3 kcal/mol free energy change from its hydrolysis is enough to be useful to drive many otherwise endergonic reactions by coupling, but it is less costly (energetically) to make than other compounds that could potentially release even more energy (e.g. phosphoenolpyruvate, PEP). Also, much of the -14.8 kcal/mol (ΔG°’) from PEP hydrolysis would be wasted because relatively few endergonic reactions are so unfavorable as to need that much free energy.

Why is ATP different from other small phosphorylated compounds? How is it that the γ-phosphoanhydride bond (the most distal) of ATP can yield so much energy when hydrolysis of glycerol-3-phosphate produces under a third of the free energy? The most obvious is electrostatic repulsion. Though they are held together by the covalent bonds, there are many negative charges in a small space (each phosphate carries approximately 4 negative charges). Removing one of the phosphates significantly reduces the electrostatic repulsion. Keeping in mind that DG is calculated from the equilibrium of both reactants and products, we also see that the products of ATP hydrolysis, ATP and phosphate, are very stable due to resonance (both ADP and Pi have greater resonance stabilization) and stabilization by hydration. The greater stability of the products means a greater free energy change.

Even when a reaction is energetically favorable (ΔG < 0), it may not occur without a little “push”, chemically speaking. The “push” is something called activation energy, and it overcomes thermodynamic stability. Consider glucose, for instance. This simple sugar is the primary source of energy for all cells and the energy inherent within its bonds is released as it breaks down into carbon dioxide and water. Since this is large molecule being broken down into smaller ones, entropy is increased, thus energy is released from reaction, and it is technically a spontaneous reaction. However, if we consider a some glucose in a dish on the lab bench, it clearly is not going to spontaneously break down unless we add heat. Once we add sufficient heat energy, we can remove the energy source, but the sugar will continue to break down by oxidation (burn) to CO₂ and H₂O.

Figure \(\PageIndex{2}\). Catalysts lower the activation energy barrier to chemical reactions without altering the free energy change for that reaction.

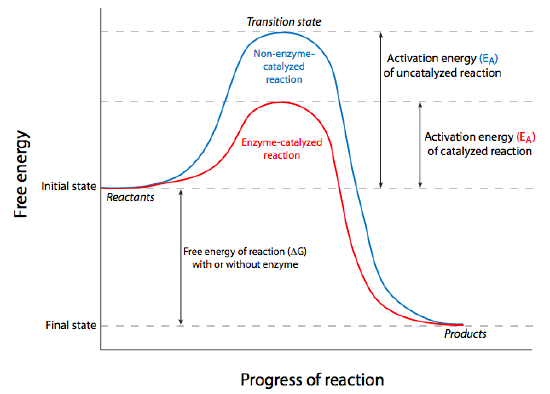
Put another way, the reactant(s) must be brought to an unstable energy state, known as the transition state (as shown at the peak of the graphs in Figure \(\PageIndex{2}\)). This energy requirement barrier to the occurrence of a spontaneous thermodynamically favored reaction is called the activation energy. In cells, the activation energy requirement means that most chemical reactions would occur too slowly/infrequently to allow for all the processes that keep cells alive because the required energy would probably come from the chance that two reactants slam into one another with sufficient energy, usually meaning they must be heated up. Again, cells are not generally able to turn on some microscopic Bunsen burner to generate the activation energy needed, there must be another way. In fact, cells overcome the activation energy problem by using catalysts for their chemical reactions. Broadly defined, a catalyst is a chemical substance that increases the rate of a reaction, may transiently interact with the reactants, but is not permanently altered by them. The catalyst can be re-used because it is the same before the reaction starts, and after the reaction completes. From a thermodynamic standpoint, it lowers the activation energy of the reaction, but it does not change the ΔG. Thus it cannot make a non-spontaneous reaction proceed; it can only make an already spontaneous reaction occur more quickly or more often.