6.4: Enzyme Inhibition
- Page ID
- 21146
Irreversible Covalent Inhibition
Given what you already know about protein structure, it should be easy to determine how to inhibit an enzyme. Since structure mediates function, anything that would significantly alter the structure of an enzyme would inhibit the activity of the enzyme. Hence extremes of pH and high temperature, all of which can denature the enzyme, would irreversibly inhibit the enzyme unless it could refold properly. Alternatively, we could add a small molecule, which interacts noncovalently with the enzyme to either change its conformation or directly prevent substrate binding. Finally, we could covalently modify certain side chains, that if they are essential to enzymatic activity, would irreversibly inhibit the enzyme.
We discussed previously the types of reagents that would chemically modify specific side chains that might be critical for enzymatic activity. For example, iodoacetamide might abolish enzyme activity if a cysteine side chain is required for activity. These reagents will usually modify several side chains, however. Determining which is critical for binding or catalytic conversion of the substrate can be difficult. One way would be to protect the active site with saturating concentrations of a ligand that binds reversibly at the active site. Then the chemical modification can be performed at varying reaction times. The critical side chain would be protected from the chemical modification with the extent of protection depending on the KD, the concentration of the protecting ligand., and the length of the reaction.
The rest of the chapter will deal with reversible, noncovalent inhibition
Competitive Inhibition
Reversible Competitive inhibition occurs when substrate (S) and inhibitor (I) both bind to the same site on the enzyme. In effect, they compete for the active site and bind in a mutually exclusive fashion. This is illustrated in the chemical equations and molecular cartoons shown in Figure \(\PageIndex{1}\).

\begin{equation}
v_0=\frac{V_M S}{K_M\left(1+\frac{I}{K is}\right)+S}
\end{equation}
There is another type of inhibition that would give the same kinetic data. If S and I bound to different sites, and S bound to E and produced a conformational change in E such that I could not bind (and vice versa), then the binding of S and I would be mutually exclusive. This is called allosteric competitive inhibition. Inhibition studies are usually done at several fixed and non-saturating concentrations of I and varying S concentrations.
The key kinetic parameters to understand are VM and KM. Let us assume for ease of equation derivation that I binds reversibly, and with rapid equilibrium to E, with a dissociation constant KIS. The "s" in the subscript "is" indicates that the slope of the 1/v vs 1/S Lineweaver-Burk plot changes while the y-intercept stays constant. KIS is also named KIC where the subscript "c" stands for competitive inhibition constant.
A look at the top mechanism shows that even in the presence of I, as S increases to infinity, all E is converted to ES. That is, there is no free E to which I could bind. Now, remember that VM= kcatE0. Under these conditions, ES = E0; hence v = VM. VM is not changed. However, the apparent KM, KMapp, will change. We can use LaChatelier's principle to understand this. If I binds to E alone and not ES, it will shift the equilibrium of E + S → ES to the left. This would increase the KMapp (i.e. it would appear that the affinity of E and S has decreased.). The double reciprocal plot (Lineweaver-Burk plot) offers a great way to visualize the inhibition as shown in Figure \(\PageIndex{2}\).

In the presence of I, VM does not change, but KM appears to increase. Therefore, 1/KM, the x-intercept on the plot will get smaller, and closer to 0. Therefore the plots will consist of a series of lines, with the same y-intercept (1/VM), and the x-intercepts (-1/KM) closer and closer to 0 as I increases. These intersecting plots are the hallmark of competitive inhibition.
Here is an interactive graph showing v0 vs [S] for competitive inhibition with Vm and Km both set to 100. Change the sliders for [I] and Kis and see the effect on the graph.
Here is the interactive graphs showing 1/v0 vs 1/[S] for competitive inhibition, with Vm and Km both set to 10.
Note that in the first three inhibition models discussed in this section, the Lineweaver-Burk plots are linear in the presence and absence of an inhibitor. This suggests that plots of v vs S in each case would be hyperbolic and conform to the usual form of the Michaelis Menton equation, each with potentially different apparent VM and KM values.
An equation for v0 in the presence of a competitive inhibitor is shown in the above figure. The only change compared to the equation for the initial velocity in the absence of the inhibitor is that the KM term is multiplied by the factor 1+I/Kis. Hence KMapp = KM(1+I/Kis). This shows that the apparent KM does increase as we predicted. KIS is the inhibitor dissociation constant in which the inhibitor affects the slope of the double reciprocal plot.
If the data were plotted as v0 vs log S, the plots would be sigmoidal, as we saw for plots of ML vs log L in Chapter 5B. In the case of a competitive inhibitor, the plot of v0 vs log S in the presence of different fixed concentrations of inhibitor would consist of a series of sigmoidal curves, each with the same VM, but with different apparent KM values (where KMapp = KM(1+I/Kis), progressively shifted to the right. Enzyme kinetic data is rarely plotted this way. These plots are mostly used for simple binding data for the M + L ↔ ML equilibrium, in the presence of different inhibitor concentrations.
Reconsider our discussion of the simple binding equilibrium, M + L ↔ ML. For fractional saturation Y vs a log L graphs, we considered three examples:
- L = 0.01 KD (i.e. L << KD), which implies that KD = 100L. Then Y = L/[KD+L] = L/[100L + L] ≈1/100. This implies that irrespective of the actual [L], if L = 0.01 KD, then Y ≈0.01.
- L = 100 KD (i.e. L >> KD), which implies that KD = L/100. Then Y = L/[KD+L] = L/[(L/100) + L] = 100L/101L ≈ 1. This implies that irrespective of the actual [L], if L = 100 Kd, then Y ≈1.
- L = KD, then Y = 0.5
These scenarios show that if L varies over 4 orders of magnitude (0.01KD < KD < 100KD), or, in log terms, from
-2 + log KD < log KD< 2 + log Kd), irrespective of the magnitude of the KD, that Y varies from approximately 0 - 1.
In other words, Y varies from 0-1 when L varies from log KD by +2. Hence, plots of Y vs log L for a series of binding reactions of increasingly higher KD (lower affinity) would reveal a series of identical sigmoidal curves shifted progressively to the right, as shown below in Figure \(\PageIndex{3}\).

The same would be true of v0 vs S in the presence of different concentrations of a competitive inhibitor, for initial flux, Jo vs ligand outside, in the presence of a competitive inhibitor, or ML vs L (or Y vs L) in the presence of a competitive inhibitor.
In many ways plots of v0 vs lnS are easier to visually interpret than plots of v0 vs S . As noted for simple binding plots, textbook illustrations of hyperbolas are often misdrawn, showing curves that level off too quickly as a function of [S] as compared to plots of v0 vs lnS, in which it is easy to see if saturation has been achieved. In addition, as the curves above show, multiple complete plots of v0 vs lnS at varying fixed inhibitor concentrations or for variant enzyme forms (different isoforms, site-specific mutants) over a broad range of lnS can be made which facilitates comparisons of the experimental kinetics under these different conditions. This is especially true if Km values differ widely.
Now that you are more familiar with binding and enzyme kinetics curves, in the presence and absence of inhibitors, you should be able to apply the above analysis to inhibition curves where the binding or the initial velocity is plotted at varying competitive inhibitor concentrations at different fixed nonsaturating concentrations of ligand or substrate. Consider the activity of an enzyme. Let's say that at some reasonable concentration of substrate (not infinite), the enzyme is approximately 100% active. If a competitive inhibitor is added, the activity of the enzyme decreases until at saturating (infinite) I, no activity would remain. Graphs showing this are shown below in Figure \(\PageIndex{4}\).

Progress Curves for Competitive Inhibition
In the previous section, we explored how important progress curve (Product vs time) analyses are in understanding both uncatalyzed and enzyme-catalyzed reactions. We are aware of no textbooks which cover progress curves for enzyme inhibition. Yet progress curves are what most investigators record and analyze to determine initial rates v0 and to calculate VM, KM and inhibition constants, as described above. We will use Vcell to produce progress curves for reversibly inhibited enzyme-catalyzed reactions.
The graphs from your initial run show the concentrations of S, P and I as a function of time for just the initial conditions shown above. In typical initial rate laboratory analyzes, of competitive inhibition, at least three sets of reactions are run with the same varying substrate concentrations and different fixed concentrations of inhibitor. In the analyses above, [I] is fixed at 5 uM.
Conduct a series of run at different values of I. Vary the KI, the dissociation constant for the EI complex, as follows:
- I << KI, the dissociation constant for the EI complex
- I >> KI, the dissociation constant for the EI complex. Then download the data and determine the initial rate for each of the initial conditions.
Figure \(\PageIndex{5}\) shows an interactive iCn3D model of human low molecular weight phosphotyrosyl phosphatase bound to a competitive inhibitor (5PNT)
Figure \(\PageIndex{5}\): Human low molecular weight phosphotyrosyl phosphatase bound to a competitive inhibitor (5PNT). (Copyright; author via source).
Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...XsEacG2tixDDi9
The competitive inhibitor, the deprotonated form of 2-(N-morpholino)-ethanesulfonic acid (MES), is actually the conjugate base of the weak acid (pKa = 6.15) of a commonly used component of a buffered solution. It is shown in color sticks with the negatively charged sulfonate sitting at the bottom of the active site pocket. The amino acids comprising the active site binding pocket are shown as color sticks underneath the transparent colored surface of the binding pocket. The normal substrates for the enzyme are proteins phosphorylated on tyrosine side chains so the sulfonate is a mimic of the negatively charged phosphate group of the phosphoprotein target.
Two specials cases of competition inhibition
Product Inhibition
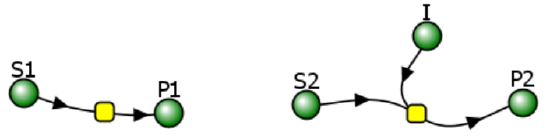
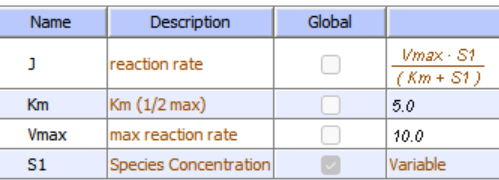
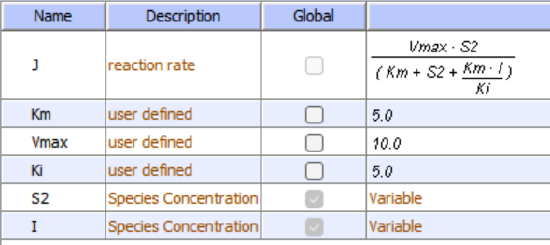
Let's look at an enzyme that converts reactant S to product P. Since P arises from S, they may have structural similarities. For example, what if GTP was the reactant and GDP was a product? If so, then P might also bind in the active site and inhibit the conversion of S to P. This is called product inhibition. It probably occurs in most enzymes, and when it does occur it will start bending downward the beginning part of the progress curve for P formation. If the product binds very tightly, it might cause a significant underestimation of the initial velocity (v0) or flux (J0) of the enzyme. Let's use Vcell to explore product inhibition. The model will explore two reactions:
- E + R ↔ ER → E + Q (no product inhibition)
- E + S ↔ ES → E + P (with product inhibition)
Note that the chemical equation above does not explicitly show the product P binding the enzyme to form an EP complex. An actual reaction diagram showing the inhibition of an enzyme by an inhibitor I and by the product P is shown in Figure \(\PageIndex{6}\) below.
Figure \(\PageIndex{6}\): reaction diagram showing inhibition of an enzyme by an inhibitor I and by the product P
Vcell uses much simpler diagrams since it is most often used for modeling whole pathways or even entire cells. In the simpler Vcell reaction diagrams, the inhibitor is typically not shown since the inhibition is built into the equation for the enzyme, represented by the node or yellow square in the figure above.
Let's now explore product inhibition in Vcell. R and Q are the reactant and product, respectively, in the reaction without product inhibition. S and P are used for the reaction with product P inhibition.
Inhibition by a competing substrate - the specificity constant
In the previous chapter, the specificity constant was defined as kcat/KM which we also described as the second-order rate constant associated with the bimolecular reaction of E and S when S << KM. It also describes how good an enzyme is in differentiating between different substrates. If an enzyme encounters two different substrates, one can be considered to be a competitive inhibitor of the other. The following equation gives the ratio of initial velocities for two competing substrates at the same concentration is equal to the ratio of their kcat/KM values.
\begin{equation}
\frac{\mathrm{v}_{\mathrm{A}}}{\mathrm{v}_{\mathrm{B}}}=\frac{\frac{\mathrm{k}_{\mathrm{catA}}}{\mathrm{K}_{\mathrm{A}}} \mathrm{A}}{\frac{\mathrm{k}_{\mathrm{cat} \mathrm{B}}}{\mathrm{K}_{\mathrm{B}}} \mathrm{B}}
\end{equation}
Here it is!
- Derivation
-
\begin{equation}
\mathrm{v}_{\mathrm{A}}=\frac{\mathrm{V}_{\mathrm{A}} \mathrm{A}}{\mathrm{K}_{\mathrm{A}}\left(1+\frac{\mathrm{B}}{\mathrm{K}_{\mathrm{B}}}\right)+\mathrm{A}} \quad \mathrm{v}_{\mathrm{B}}=\frac{\mathrm{V}_{\mathrm{B}} \mathrm{B}}{\mathrm{K}_{\mathrm{B}}\left(1+\frac{\mathrm{A}}{\mathrm{K}_{\mathrm{A}}}\right)+\mathrm{B}}
\end{equation}\begin{equation}
\frac{\mathrm{v}_{\mathrm{A}}}{\mathrm{v}_{\mathrm{B}}}=\frac{\frac{\mathrm{V}_{\mathrm{A}} \mathrm{A}}{\mathrm{K}_{\mathrm{A}}\left(1+\frac{\mathrm{B}}{\mathrm{K}_{\mathrm{B}}}\right)+\mathrm{A}}}{\frac{\mathrm{V}_{\mathrm{B}} \mathrm{B}}{\mathrm{K}_{\mathrm{B}}\left(1+\frac{\mathrm{A}}{\mathrm{K}_{\mathrm{A}}}\right)+\mathrm{B}}}=\frac{\frac{\mathrm{V}_{\mathrm{A}} \mathrm{A}}{\mathrm{K}_{\mathrm{A}}+\frac{\mathrm{K}_{\mathrm{A}} \mathrm{B}}{\mathrm{K}_{\mathrm{B}}}+\mathrm{A}}}{\frac{\mathrm{V}_{\mathrm{B}} \mathrm{B}}{\mathrm{K}_{\mathrm{B}}+\frac{\mathrm{K}_{\mathrm{B}} \mathrm{A}}{\mathrm{K}_{\mathrm{A}}}+\mathrm{B}}}
\end{equation}Now in the above equation:
multiple the top half of the right-hand expression by \begin{equation}
\frac{\frac{1}{K_A}}{\frac{1}{K_A}}
\end{equation} multiple the bottom half of the right-hand expression by \begin{equation}
\frac{\frac{1}{K_B}}{\frac{1}{K_B}}
\end{equation} replace VA with kcatAE0 and VB with kcatBE0This gives the following expression for vA/vB:
\begin{equation}
\frac{\mathrm{v}_{\mathrm{A}}}{\mathrm{v}_{\mathrm{B}}}=\frac{\frac{\mathrm{k}_{\mathrm{catA}}}{\mathrm{K}_{\mathrm{A}}} \mathrm{A}}{\frac{\mathrm{k}_{\mathrm{cat} \mathrm{B}}}{\mathrm{K}_{\mathrm{B}}} \mathrm{B}}
\end{equation}
Uncompetitive Inhibition
Reversible uncompetitive inhibition occurs when I binds only to ES and not free E. One can hypothesize that on binding S, a conformational change in E occurs which presents a binding site for I. Inhibition occurs since ESI can not form the product. It is a dead-end complex that has only one fate, to return to ES. This is illustrated in the chemical equations and molecular cartoon shown in Figure \(\PageIndex{7}\).

\begin{equation}
v_0=\frac{V_M S}{K_M+S\left(1+\frac{I}{K i i}\right)}=\frac{\left(\frac{V_M}{1+\frac{I}{K i i}}\right) S}{\left(\frac{K_M}{1+\frac{I}{K i i}}\right)+S}
\end{equation}
Let us assume that I binds reversibly to ES with a dissociation constant Kii. The second "i" in the subscript "ii" indicates that the intercept of the 1/v vs 1/S Lineweaver-Burk plot changes while the slope stays constant. Kii is also named Kiu, where the subscript "u" stands for the uncompetitive inhibition constant.
A look at the top mechanism shows that in the presence of I, as S increases to infinity, not all of E is converted to ES. That is, there is a finite amount of ESI, even at infinite S. Now remember that Vm = kcatE0 if and only if all E is in the form ES. Under these conditions, the apparent Vm, Vmapp is less than the real Vm without the inhibitor. In addition, the apparent Km, Kmapp, will change. We can use LaChatelier's principle to understand this. If I binds to ES alone, and not E, it will shift the equilibrium of E + S ↔ ES to the right, which would have the effect of decreasing the Kmapp (i.e. it would appear that the affinity of E and S has increased.). The double reciprocal plot (Lineweaver Burk plot) offers a great way to visualize the inhibition. In the presence of I, both Vm and Km decrease. Therefore, -1/Km, the x-intercept on the plot, will get more negative, and 1/Vm will get more positive. It turns out that they change to the same extent. Therefore the plots will consist of a series of parallel lines, which is the hallmark of uncompetitive inhibition, as shown in Figure \(\PageIndex{8}\).

Here is an interactive graph showing v0 vs [S] for uncompetitive inhibition with Vm and Km both set to 100. Change the sliders for [I] and Kis and see the effect on the graph.
Here is an interactive graph showing uncompetitive inhibition with Vm and Km both set to 10. Change the sliders for [I] and Kii and see the effect on the graph
An equation, shown in the diagram above, can be derived which shows the effect of the uncompetitive inhibitor on the velocity of the reaction. The only change is that the S term in the denominator is multiplied by the factor 1+I/Kii. We would like to rearrange this equation to show how Km and Vm are affected by the inhibitor, not S, which obviously isn't. Rearranging the equation above shows that Kmapp = Km/(1+I/Kii) and Vmapp = Vm/(1+I/Kii). This shows that the apparent Km and Vm do decrease as we predicted. Kii is the inhibitor dissociation constant in which the inhibitor affects the intercept of the double reciprocal plot. Note that if I is zero, Km and Vm are unchanged.
Progress Curves: Uncompetitive Inhibition
Now let's compare the progress curves for an enzyme-catalyzed reaction in the absence and presence of an uncompetitive inhibitor.
Figure \(\PageIndex{9}\) shows an interactive iCn3D model of an uncompetitive inhibitor of the cysteine protease caspase-6 (4HVA)
Figure \(\PageIndex{9}\): Uncompetitive inhibitor of the cysteine protease caspase-6 (4HVA) . (Copyright; author via source).
Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...TVfKio7NxcpX28
The "substrate" in this model (cyan, transparent surface, with labels on V, E, and I) is a substrate analog, VEI-CHO in which the tripeptide substrate VEI ends not in a free carboxyl or amide group but an aldehyde, which causes this "substrate" to become covalently attached to the enzyme and act as an inhibitor. The uncompetitive inhibitor (gray transparent surface) binds externally to the blue surface. Hence it binds to the ES complex. Two active site residues, Cys 163, the active site nucleophile, and His 121, a catalytic acid/base are shown in colored sticks and labeled.
Figure \(\PageIndex{10}\) below shows a Lineweaver-Burk plot showing 1/vo vs 1/[S], where the substrate is the divalent compound (VEID)2R110. Its N-terminus is capped with a benzyloxy (Z) group. R110 is a rhodamine-type fluorophore, which on cleavage gives a strong fluorescent signal that was initially quenched by the benzyloxy group in the uncleaved substrate.
Figure \(\PageIndex{10}\): Double-reciprocal Lineweaver-Burk plot of compound 3 with (VEID)2R110 substrate showing uncompetitive inhibition. Heise CE et al. (2012) Mechanistic and Structural Understanding of Uncompetitive Inhibitors of Caspase-6. PLoS ONE 7(12): e50864. https://doi.org/10.1371/journal.pone.0050864. Creative Commons Attribution License.
Noncompetitive and Mixed Inhibition
Reversible noncompetitive inhibition occurs when I binds to both E and ES. We will look at only the special case in which the dissociation constants of I for E and ES are the same. This is called noncompetitive inhibition. It is quite rare as it would be difficult to imagine a large inhibitor that inhibits the turnover of a bound substrate having no effect on the binding of S to E. However covalent interaction of protons with both E and ES can lead to noncompetitive inhibition. In the more general case, the Kd's are different, and the inhibition is called mixed. Since inhibition occurs, we will hypothesize that ESI can not form the product. It is a dead-end complex that has only one fate, to return to ES or EI. This is illustrated in the chemical equations and in the molecular cartoon in Figure \(\PageIndex{11}\).
Let us assume for ease of equation derivation that I binds reversibly to E with a dissociation constant of Kis (as we denoted for competitive inhibition) and to ES with a dissociation constant Kii (as we noted for uncompetitive inhibition). Assume for noncompetitive inhibition that Kis = Kii. A look at the top mechanism shows that in the presence of I, as S increases to infinity, not all of E is converted to ES. That is, there is a finite amount of ESI, even at infinite S. Now remember that Vm = kcatE0 if and only if all E is in the form ES . Under these conditions, the apparent Vm, Vmapp is less than the real Vm without an inhibitor. In contrast, the apparent Km, Kmapp, will not change since I binds to both E and ES with the same affinity, and hence will not perturb that equilibrium, as deduced from LaChatelier's principle. The double reciprocal plot (Lineweaver Burk plot) offers a great way to visualize the inhibition. In the presence of I, just Vm will decrease. Therefore, -1/Km, the x-intercept will stay the same, and 1/Vm will get more positive. Therefore the plots will consist of a series of lines intersecting on the x-axis, which is the hallmark of noncompetitive inhibition. You should be able to figure out how the plots would appear if Kis is different from Kii (mixed inhibition).
\begin{equation}
v_0=\frac{V_M S}{K_M\left(1+\frac{I}{K i s}\right)+S\left(1+\frac{I}{K i i}\right)}
\end{equation}
An equation, shown in the diagram above can be derived which shows the effect of the noncompetitive inhibitor on the velocity of the reaction. In the denominator, Km is multiplied by 1+I/Kis, and S by 1+I/Kii. We would like to rearrange this equation to show how Km and Vm are affected by the inhibitor, not S, which obviously isn't. Rearranging the equation as shown above shows that Kmapp = Km(1+I/Kis)/(1+I/Kii) = Km when Kis=Kii, and Vmapp = Vm/(1+I/Kii). This shows that the Km is unchanged and Vm decreases as we predicted. The plot shows a series of lines intersecting on the x-axis as shown in Figure \(\PageIndex{12}\). Both the slope and the y-intercept are changed, which are reflected in the names of the two dissociation constants, Kis and Kii. Note that if I is zero, Kmapp = Km and Vmapp = Vm. Sometimes the Kis and Kii inhibition dissociation constants are referred to as Kc and Ku (competitive and uncompetitive inhibition dissociation constants.

Move the sliders on this interactive graph below to show changes in Kis and Kii affect position on the graph where the lines intersect. Try to change their values to move the intersections of the graphs from the left top quadrant to the x-axis to the left bottom quadrant.
Here is an interactive graph showing v0 vs [S] for mixed inhibition with Vm and Km both set to 100. Change the sliders for [I] and Kis and see the effect on the graph
Here is an interactive graph showing mixed inhibition with Vm and Km both set to 10. Change the sliders for [I] and Kii and see the effect on the graph
Progress Curves: Mixed/Noncompetitive Inhibition
Now let's compare the progress curves for an enzyme-catalyzed reaction in the absence and presence of a mixed inhibitor.
Mixed and noncompetitive inhibition (as shown by the mechanism above) differ from competitive and uncompetitive inhibition in that the inhibitor binding is not simply a dead-end reaction in which the inhibitor can only dissociate in a single reverse step. In the above equilibrium, S can dissociate from ESI to form EI so the system may not be at equilibrium. With dead-end steps, no flux of reactants occurs through the dead-end complex so the equilibrium for the dead-end step is not perturbed.
Other mechanisms can commonly give mixed inhibition. For example, the product released in a ping pong mechanism (discussed in the next chapter) can give mixed inhibition. A ping pong reaction mechanism is shown and superficially explained in Figure \(\PageIndex{13}\).

If P, acting as a product inhibitor, can bind to two different forms of the enzyme (E' and also E), it will act as a mixed inhibitor.
Figure \(\PageIndex{14}\) shows an interactive iCn3D model of a noncompetitive inhibitor of M. tuberculosis's class IIa fructose 1,6-bisphosphate aldolase (4LV4).
Figure \(\PageIndex{14}\): Noncompetitive inhibitor of M. tuberculosis's class IIa fructose 1,6-bisphosphate aldolase (4LV4). (Copyright; author via source).
Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...wZDtkvtwqnrVy7
The non-competitive inhibitor, 8-hydroxyquinoline carboxylic acid (HCA), is shown as with a cyan surface. Active site side chains of the Zn2+- containing enzyme are shown as colored sticks and labeled.
The noncompetitive inhibitor does not enter into the pocket where the substrate (not shown in the model above) binds. The binding of the noncompetitive inhibitor causes a conformational change that moves the Zn-binding loop (Z-loop) which contains His 212 which coordinates the Zn2+ ion. Hence the Zn-loop is part of the active site and when it moves on binding of the inhibitor, the access to the empty pocket where the substrate binds is hindered. When the Zn2+ moves away from the active site, it can no longer engage in catalytic activity.
Enzyme Inhibition in Vivo
The pharmaceutical industry is devoted to finding drug molecules that affect biological processes. Typically this means the development of small molecule inhibitors of target proteins. Recent work has expanded to the development of inhibitory RNA molecules that affect DNA transcription and mRNA translation. Using combinatorial synthetic techniques and computational modeling, it has gotten easier to develop small molecule inhibitors (especially competitive ones) that inhibit proteins in vitro using purified enzymes, substrates, and inhibitors in lab testing. Assuming that the inhibitor could pass through the membrane and accumulate to a sufficient enough concentration, would it have the same inhibitory properties in the cell as in the test tube? The answer turns out to be maybe. Remember that a cell is tightly packed with a multitude of other small molecules and macromolecules. In addition, the enzyme targeted for inhibition is most likely part of a pathway of enzymes that feeds reactant into the enzyme and removes the product. Hence, the flux of substrate and product is controlled by the entire pathway and not just the single target enzyme. The concentration of the product of the target enzyme is determined by kinetic parameters for the enzyme and available substrate concentration.
The conditions under which the enzymes are studied (in vitro) and operate (in vivo) are very different.
- In vitro (in the lab), the enzyme is held at a constant concentration while the substrate is varied (i.e the substrate concentration is the independent variable). The velocity is determined by the substrate concentration. When inhibition is studied, the substrate is varied while the inhibitor is held constant at several different fixed concentrations.
- In vivo (in the cell), the velocity might be held at a relatively fixed level with the substrate determined by the velocity. To avoid a bottleneck in flux, the substrate can't build up at the enzyme, so the enzyme processes it in a steady state fashion to produce the product as determined by the Michael-Menten equation.
What happens when an inhibitor is added in vivo? Let's assume that the enzyme is running at v = Vm/2. How might in vivo inhibition plots look at constant velocity (for example v=Vm/2) when both I and S can vary and in which S for an enzyme in the middle of a pathway is determined by v?
The equations and graph below show the ratio of S/Km vs I/Kix for inhibition at constant v, a condition encountered when an enzyme in a metabolic pathway is subject to flux controls imposed by the entire pathway. The x-axis reflects the ratio of inhibitor concentration to its inhibition constant. Likewise, the y-axis reflects the relative amount of substrate compared to its Km. The graph for in vivo competitive inhibition is linear, but it "blows up" for uncompetitive inhibition as shown in Figure \(\PageIndex{15}\).
Here are derivations used to produce the graphs in Figure \(\PageIndex{13}\).
Here it is!
- Derivation
-
Competitive Inhibition at constant velocity v:
Let's start with the equation of competitive inhibition.
\begin{equation}
\mathrm{v}=\frac{\mathrm{V}_{\mathrm{M}} \mathrm{S}}{\mathrm{K}_{\mathrm{M}}\left(1+\frac{\mathrm{I}}{\mathrm{K}_{\mathrm{is}}}\right)+\mathrm{S}}
\end{equation}Let
\begin{equation}
\left(1+\frac{\mathrm{I}}{\mathrm{K}_{\mathrm{is}}}\right)=\mathrm{y}
\end{equation}Then,
\begin{equation}
\begin{gathered}
v=\frac{V_M S}{K_M y+S} \\
v\left(K_M y+S\right)=V_M S \\
v K_M y+v S=V_M S \\
v K_M y=V_M S-v S=S\left(V_M-v\right) \\
K_M=\frac{S\left(V_M-v\right)}{v y}
\end{gathered}
\end{equation}which gives:
\begin{equation}
\begin{gathered}
\frac{S}{K_M}=\frac{v y}{\left(V_M-v\right)}=\frac{y}{\frac{V_M}{v}-1}=\frac{1+\frac{I}{K_{i s}}}{\frac{V_M}{v}-1}=\frac{1}{\frac{V_M}{v}-1}+\frac{\frac{I}{K_{i s}}}{\frac{V_M}{v}-1} \\
\frac{S}{K_M}=\frac{1}{\frac{V_M}{v}-1}+\left(\frac{1}{\frac{V_M}{v}-1}\right) \frac{I}{K_{i s}}
\end{gathered}
\end{equation}Note from the last equation that the graph of S/KM vs I/Kis is linear (at a fixed v), as shown in the above figure.
Uncompetitive Inhibition at constant velocity v:
Let's start with the equation of uncompetitive inhibition.
\begin{equation}
\mathrm{v}=\frac{\mathrm{V}_{\mathrm{M}} \mathrm{S}}{\mathrm{K}_{\mathrm{M}}+\mathrm{S}\left(1+\frac{\mathrm{I}}{\mathrm{K}_{\mathrm{ii}}}\right)}
\end{equation}Let
\begin{equation}
\left(1+\frac{1}{\mathrm{K}_{\mathrm{ii}}}\right)=\mathrm{y}
\end{equation}then:
\begin{equation}
\begin{gathered}
v=\frac{V_M S}{K_M+S y} \\
v\left(K_M+S y\right)=V_M S \\
v K_M=V_M S-v S y=S\left(V_M-v y\right)
\end{gathered}
\end{equation}which gives:
\begin{equation}
\frac{S}{K_M}=\frac{v}{V_M-v y}\left(\frac{\frac{1}{v}}{\frac{1}{v}}\right)=\frac{1}{\frac{V_M}{v}-y}=\frac{1}{v-1-\frac{I}{K_{i i}}}
\end{equation}This graph is not a linear function of I/Kii as it was for in vivo competitive inhibition.
- for competitive inhibition, the graph of S/KM is a linear function of I/Kis
- for uncompetitive inhibition, the graph of S/KM is NOT a linear function of I/Kii but rather "blows up" to infinity.
These graphs and associated equations are dramatically different from the very similar forms of inhibition equations and curves for in vitro inhibition at varying S and different fixed values of inhibitor. Consider the uncompetitive graph and equation. In the absence of an inhibitor, if S=Km, then Vm/v = 2 so the calculated value from the equation above of S/Km = 1. The y-intercept of the graph above is 1 for uncompetitive (and competitive) inhibition. If I is allowed to increase to a value of Kii (so I/Kii = 1), again at constant v=Vm/2, then the right-hand side goes to infinity.
In a linked series of reactions, if the middle reaction is inhibited, the substrate for that enzyme builds, whether the inhibition is competitive or uncompetitive. With competitive inhibition, the substrate concentration can be raised to meet the requirements of the enzyme. But as the above figure shows, this can't happen for uncompetitive inhibition since as more substrate accumulates, the reaction reaches a point where the steady state is lost.
Obviously, this limiting case can't be realistically reached but it does suggest that uncompetitive inhibitors would be more effective in vivo in controlling a metabolic pathway than competitive inhibitors. Cornish-Bowden argues that purely uncompetitive inhibitors are rare in nature because of the degree of inhibition they can hypothetically produce (1986). Likewise, he suggests that medicinal chemists should synthesize uncompetitive inhibitors if their goal is to maximally inhibit a metabolic pathway under the kind of flux control described above. Although it is more difficult to synthesize a purely uncompetitive inhibitor (as it can't be easily modeled after the structure of a natural ligand that binds to the active site and are competitive inhibitors), he notes that synthesizing mixed (and noncompetitive) inhibitors whose Kii values are of reasonable size compared to their Kis values, would be one approach.
Move the sliders on the interactive graph below to show how the graphs change. Disregard the graph in the right lower quadrant as that location would require negative values of either S or K.
Inhibition by Temperature and pH Changes
From 0 to about 40-50o C, enzyme activity usually increases, as do the rates of most reactions in the absence of catalysts. (Remember the general rule of thumb that reaction velocities double for each increase of 10oC.). At higher temperatures, the activity decreases dramatically as the enzyme denatures. These features are illustrated in Figure \(\PageIndex{16}\).

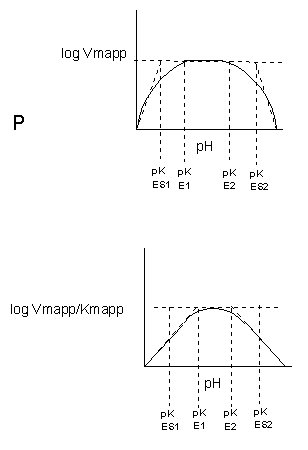
Likewise, pH has a marked effect on the velocity of enzyme-catalyzed reactions as illustrated in Figure \(\PageIndex{17}\).

Think of all the things that pH changes might affect. It might
- affect E in ways to alter the binding of S to E, which would affect Km
- affect E in ways to alter the actual catalysis of bound S, which would affect kcat
- affect E by globally changing the conformation of the protein
- affect S by altering the protonation state of the substrate
The easiest assumption is that key side chains necessary for catalysis must be in the correct protonation state. Thus, a sidechain, with an apparent pKa of around 6, must be deprotonated for optimal activity of trypsin which shows increases in activity with pH centered at pH 6. Which amino acid side chain would be a likely candidate?
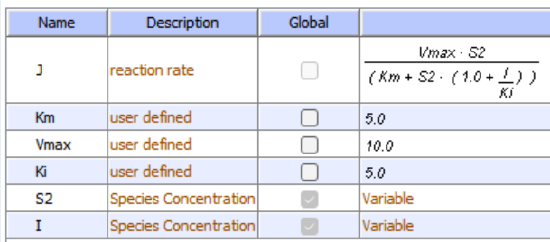
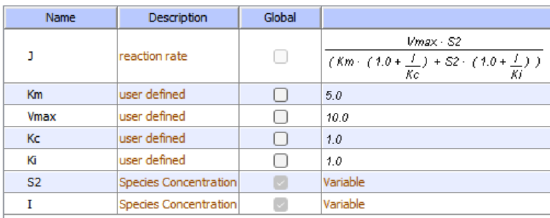
Table \(\PageIndex{1}\) below shows how pH effects on enzyme kinetics can be modeled at the chemical and mathematical level.
|
\begin{equation} |
 |





.png?revision=1&size=bestfit&width=390&height=330)
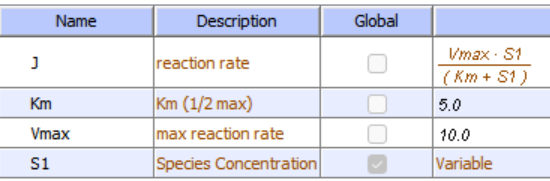
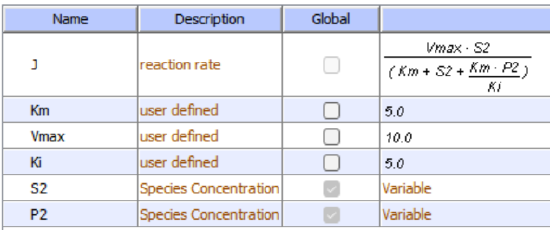
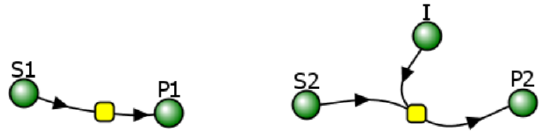
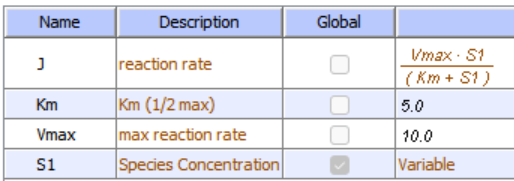
.png?revision=1&size=bestfit&width=353&height=323)
.png?revision=1&size=bestfit&width=372&height=299)