5.3: Oxygen-Binding Proteins and Allosterism
- Page ID
- 14941
Myoglobin, Hemoglobin, and their Ligands
Almost all biochemistry textbooks start their description of the biological functions of proteins using myoglobin and hemoglobin as exemplars. On the surface this is a rational approach since they have become model systems to describe the binding of simple ligands, like dioxygen (O2), CO2, and H+, and how the structure of a protein determines and is influenced by binding of ligands.
Yet in most ways, these globin-binding "ligands" are dissimilar to the majority of both small ligands, such as substrates (for enzymes), inhibitors and activators as well as large "ligands", such as other proteins, nucleic acids, carbohydrates and lipids that bind to proteins through noncovalent interactions (described in detail in Chapter 2.4). In contrast, dioxygen (O2), CO2, and H+ bind reversibly, but through covalent interactions. Dioxygen binds to a heme Fe2+ transition metal through a coordinate covalent or dative bond, protons obviously bind covalently to proton acceptors (Lewis bases like histidine), while CO2 binds covalently as it forms a carbamate with the N terminus of a hemoglobin chain. In typical covalent bonds, each bonded atom contributes to and shares the two electrons in the bond. In coordinate or dative covalent bonds, the ligand, a Lewis base, contributes both electrons in the bond. For simple analyses and four counting electrons, both electrons can be considered to be "owned" by the ligand and not by the transition metal ion, a Lewis acid, unless you analyze the interactions using molecular orbital (ligand field) theory. Hence the ligand can readily dissociate from the metal ion, much as a ligand bound through classical noncovalent interactions does. This analogy can be extended to protons which are also Lewis acids (with no contributing electrons) as they react with Lewis bases (lone pair donors) on atoms such as nitrogen on a histidine side chain. H+ readily leave (ionize) from a Lewis acid if the pH of the microenvironment is conducive to ionization.
Even though we disagree with starting the discussion of protein structure and function with the covalent binding of small gaseous and marginally soluble ligands to myoglobin and hemoglobin, we will anyway to make the book consistent with most other texts and allow easier use without shuffling the order of chapters.
Let's start with myoglobin (Mb), a monomeric protein containing 8 α−helices (A-H) and with hemoglobin, a heterotetramer with two α -and two β−subunits, each which also contains 8 α−helices. Both are oxygen binding proteins. Both contain heme (one in myoglobin, and 4 for the four subunits of hemoglobin). Each heme has a central Fe2+ ion, which forms a coordinate covalent bond with dioxygen. Dioxygen is transported from lungs, gills, or skin of animals to the capillaries, where it can be delivered to respiring tissue. O2 has a low solubility in blood (0.1 mM). Whole blood contains 150 g Hb/L, and can achieve a dissolved oxygen concentration of 10 mM. Invertebrates can have alternative proteins for oxygen binding, including hemocyanin, which contains Cu and hemerythrin, a non-heme protein. On binding dioxygen, solutions of Hb change color to bright red. Solutions of hemocyanin and hemerythrin change to blue and burgundy colored, respectively, on binding dioxygen. Some Antarctic fish don't require Hb since dioxygen is more soluble at low temperatures. Myoglobin is found in the muscles, and serves as a storage protein for oxygen transported by hemoglobin.
The structure of heme in myoglobin and hemoglobin, is shown in Figure \(\PageIndex{1}\).
The heme group contains protoporphyrin IX, with four tetrapyrrole rings linked by methene bridges. Attached to the tetrapyrrole structure are four methyl, two vinyl, and two propionate groups. These can be arranged in 15 ways, of which only one (IX) occurs in biological systems. Protoporphyrin IX with bonded ferrous (Fe2+) iron is called heme and has a nitrogen atom on each of the four pyrrole rings that form a coordinate covalent bond to Fe2+. The heme fits into a hydrophobic crevice in heme-bindin proteins with the propionate groups exposed to solvent.
Myoglobin (Mb)
Myoglobin is an extremely compact protein with 75% alpha helical structure. It has 8 α−helices labeled A-H. Four are terminated by a proline, a helix breaker. The interior amino acids are almost entirely nonpolar. The only polar amino acids found completely buried are two histidines. One is called the proximal His as it is nearer the heme and serves the 5th ligand to the heme Fe2+. The other is called the distal His, which is too far to coordinate the heme Fe2+. This last potential 6th ligand-binding site forms a coordinate covalent bond with O2 in oxy-myoglobin.
Figure \(\PageIndex{2}\) shows an interactive iCn3D model of deoxymyoglobin from wild boar. The heme is shown in sticks along with the proximal and distal histidines.
.png?revision=1&size=bestfit&width=242&height=238)
Hemoglobin
Hemoglobin has an illustrious history. It is the first protein whose molecular weight was determined and the first assigned a specific function (dioxygen transport). It was the first protein in which a mutation in a single amino acid caused by a single base pair change in the DNA coding sequence was shown to cause a disease (sickle cell trait and disease). The mathematical theories developed to model dioxygen binding are used to explain enzyme activity. It also binds H+, CO2, and bisphosphoglcyerate which bind to sites (allosteric) distant from the oxygen binding site which regulates its dioxygen binding affinity.
As with myoglobin, the Fe2+ ion is coordinated to 4 Ns on the 4 pyrrole rings, The 5th ligand is supplied by proximal His (the 8th amino acid on helix F) of the protein. In the absence of dioxygen, the 6th ligand is missing. and the geometry of the complex is somewhat square pyramidal, with the Fe slightly above (0.2 Å) the plane of the heme ring. A distal His (E7) is on the opposite side of the heme ring, but too far to coordinate with the Fe2+. When dioxygen binds, it occupies the 6th coordination site and pulls the Fe into the plane of the ring, leading to octahedral geometry. These changes that occur on oxygenation are shown in Figure \(\PageIndex{3}\).
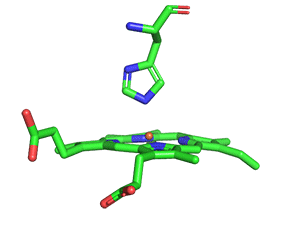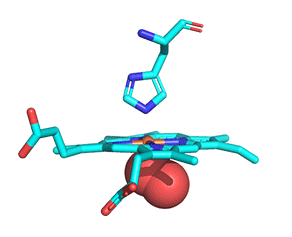
The proximal histidine that provides the imidazole nitrogen ligand is shown. Dioxygen is shown as red spheres. Fe2+ ion is shown as a small orange sphere. Its size has been dramatically reduced in this image so its movement can be more readily observed.
Carbon monoxide (CO), nitric oxide (NO), and hydrogen sulfide (H2S) also bind to the sixth coordination site, but with higher affinity than dioxygen, which can lead to CO poisoning for example. The distal histidine keeps these ligands (including dioxygen) bound in a bent, non-optimal geometry. This minimizes the chances of CO poisoning.
Figure \(\PageIndex{4}\) shows an interactive iCn3D model of human oxy-hemoglobin (2dn1)
Fe2+ ion ligand interactions
When the 6th ligand, dioxygen, binds to heme Fe2+, the geometry of the complex becomes octahedral. The Fe2+ ion has 6 electrons in d orbitals. The electronic configuration of atomic Fe is 3d64s2 while the Fe2+ ion has a 3d6 configuration, as shown in Figure \(\PageIndex{5}\). Each of the orbitals would have the same energy except for the doubly occupied one which would have slightly higher energy due to the extra repulsion of the two electrons in the orbital. This effect is minimal so to a first approximation, the orbitals are considered to have the same energies (they are degenerate). The figure below shows them having the same energy
You will remember from introductory chemistry classes that transition metal complexes and their solutions are highly colored. Since oxygenated hemoglobin (found in arteries) appears bright red/orange, it must absorb blue/green light more than deoxyhemoglobin, which is darker red (but still reddish). These absorbed wavelengths are removed from the spectrum, making hemoglobins shades of red. Veins contained more deoxygenated blood returning to the heart to be reoxygenated. The visible veins in your arms and legs appear blue not because of the spectral properties of deoxyhemoglobin. Rather, blue light doesn't penetrate into the tissue as far as red, so red is preferentially removed from the remaining light which is reflected, making veins appear blue. Figure \(\PageIndex{6}\) shows a partial absorbance spectrum of deoxy- and oxy-hemoglobin from 280-1000 nm.
The dashed light blue vertical line shows the approximate wavelength (around 450 nm) of the largest molar extinction coefficient difference between the two forms. Note that the y axis is a log scale. At 450 nm, oxyhemoglobin has an extinction coefficient of about 600,000 while deoxyhemoglobin is about 60,000, so much more blue light is removed from a solution of oxyHb, making it appear bright red. Note also that the same differences appear in the red region of the spectra, where the extinction coefficients only vary from 3000 for oxyhemoglobin to 200 for deoxyHb. Hence absorption in this region has little effect on the visible color of blood.
The spectrum shown in Figure \(\PageIndex{6}\) also shows the near-infrared region (denoted by a rectangle) of the spectra. Inexpensive pulse oximeters (some built into watches) have been increasingly used by people at home to their measure their oxygenation status during the COVID-19 pandemic. These use two pulsed LEDs, one at 660 nm, where oxyhemoglobin has a higher extinction coefficient, and one at 940 (infrared region), where deoxyhemoglobin has a higher extinction coefficient.
Binding of ligand to the heme Fe2+: crystal and ligand fields
Most biochemistry books offer minimal coverage of bioinorganic chemistry, even though a large percentage of proteins bind metal ions. Since biochemistry is an interdisciplinary field, it is important to use past learning in other biology and chemistry courses and apply it to biochemistry. Most students study transition metal chemistry in introductory chemistry courses. You should familiar with transition metal ions, their electronic configuration, crystal field theory, high and low spin states, paramagnetism and diamagnetism. Hence it is appropriate and important to bring these ideas into biochemistry and extend them when necessary. The basis of the material below is modified from Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller (Creative Commons Attribution-NonCommercial 3.0 Unported License).
Let's look at the electronic structure of Fe2+ in oxyhemoglobin. The Fe2+ is coordinated to six ligands (4 pyrrole rings of the heme in a plane, one axial imidazole ring each from the proximal histidine and bonded dioxygen). The geometry of the electron clouds around the Fe2+ is octahedral. The six d orbitals are oriented in the same x, y, and z axes direction as the heme ligands. This geometry and the shapes and orientations of the Fe2+ d atomic orbitals are illustrated in Figure \(\PageIndex{7}\).
Two of the orbitals, dz2 and dx2-y2, appear different in that they are oriented directly along the x, y and z axes while the other three are in-between the axes. Now imagine six anionic ligands with lone pairs approaching along the axes of the Fe2+ atomic orbitals, a postulate of crystal field theory used to explain bonding in transition metal complexes. The energy of the Fe electrons in the dz2 and dx2-y2 atomic orbitals would be raised higher than the others due to electron-electron repulsion. This is illustrated in Figure \(\PageIndex{8}\). Two different outcomes can arise
1 (left panel): If the electrostatic interaction between the atomic orbitals of the Fe ion and the incoming ligands is low, the energy of the dz2 and dx2-y2 orbitals would be a bit higher (by an amount Δ) due to the great repulsion along those axes from anions oriented along them. This is illustrated in the left part of Figure \(\PageIndex{8}\). When filling the orbitals with the six Fe2+ 3d6 electrons, you would add one electron to each of the 5 orbitals and then pair one for the sixth orbital. In that case there would be 4 unpaired electrons and the complex would be paramagnetic. We call this a high spin state.
2 (right panel): If however, the electrostatic interactions of the incoming ligands with the d atomic orbital electrons is high, the Δ would be large. When filling the orbitals in this case with the six Fe2+ 3d6 electrons, the electron would be paired in the three lower energy orbitals and there would be no electrons unpaired, so the ion is diamagnetic. This is the low spin case.
In either case, if light of energy equal to the Δ interacts with the metal ion, electrons would be promoted to the higher energy level. For the low spin case (larger axial electrostatic interactions, Δ is large, the energy of the required photon is larger (more blue shifted) than in the high spin case. This could make a solution of the molecule in the low spin case appear redder than for the high spin case (as blue light is removed on absorption). This is the case for dioxygen, which interacts strongly with the Fe2+ axially-oriented orbitals. Hence oxy-Fe2+ heme complex is low spin and diamagnetic.
You studied basic crystal field theory in introductory chemistry courses. The theory is simplistic in several ways. The ligands might not be anions. More importantly, bonding is best described by molecular orbitals. A more comprehensive ligand field theory takes into account the effect of the donor electrons and the d orbitals of the transition metal ion. These atomic orbitals combine to produce molecular orbitals (MOs), which better describes bonding.
Take the simple case of a covalent bond between two singly occupied adjacent p atomic orbitals the two carbons of ethylene (C2H4). Simplistically, you could imagine two carbon atoms with their two p orbitals approaching each other. The two p orbitals (or more accurately their wave functions) could combine constructively or destructively to form two new molecular orbitals (MO). One is a pi bonding MO, π, which is lower in energy (promoting bond formation) than the atomic p orbitals. The other is a pi antibonding MO, π*, which is higher in energy (antagonizing bond formation), as shown in Figure \(\PageIndex{9}\). Two atomic orbitals form from two MOs!
Let's use ligand field theory with its MOs to describe ligands binding to the heme Fe2+ d orbitals. This is illustrated in the MO diagram in Figure \(\PageIndex{10}\).
Figure \(\PageIndex{10}\): Ligand field molecular orbtials for the d6 Fe2+ ion for two axial ligands
For simplicity, for Fe2+ we will consider only d orbitals and focus on the dz2 and dx2-y2 (also called the eg) orbitals, since these are most affected by the ligands as described in crystal field theory. Let's assume these interact with lone pairs (a simplistic assumption as well) in two ligand orbitals, one on the dioxygen and one on the proximal histidine imidazole N. Seven atomic orbitals (5 Fe d2+ orbitals and 2 ligand orbitals) combine to produce 7 MOs. Since the orbitals (in sp2- or sp3-like orbitals) on the ligands are closer in energy to the lower energy bonding MOs, their electrons would go there. Since O2 interacts strongly with the Fe2+ d orbitals, the system is in a low spin state, with the unoccupied dz2 and dx2-y2 (eg orbitals) now considered antibonding orbitals. The fully occupied dxy, dxz and dyz are considered nonbonding orbitals since they have the same relative energy atomic orbitals.
We will return to molecular orbitals occasionally throughout this book when they offer the best explanation for biological events.
Here are some important things to note. When dioxygen binds to the heme iron, the oxidation state of the Fe2+ ion does not change, even though dioxygen is a great oxidizing agent. Hence the Fe2+ ion is a reversible carrier of dioxygen not of electrons. Free heme in solution is oxidized by dioxygen, forming a complex with water which occupies the 6th position, with the iron in the Fe3+ state. An intermediate in this process is the formation of a dimer of 2 hemes linked by 1 dioxygen. This can't occur readily when the heme is in Hb or Mb. Other heme proteins (like Cytochrome C), which we will explore in future chapters, are designed to be carriers of electrons. A small amount of the Fe2+ ion can get oxidized to Fe3+ ion myoglobin and hemoglobin, resulting in met-Hb and met-Mb. The brown color of old meat results in large part from Met-Mb. A enzyme is required to reduced the iron back to the Fe2+ state.
The differences between hemoglobin and myoglobin are equally important. Hemoglobin is a heterotetramer of two α and two β subunits held together by noncovalent interactions (an example of quaternary protein structure), with 4 bound hemes, each of which can bind a dioxygen. In a fetus, two other subunits make up hemoglobin (two zeta - ζ and two epsilon - ε subunits -analogous to the two α and two β subunits, respectively). This changes in development to two α and two γ subunits. Fetal hemoglobin has a higher affinity for dioxygen than does adult hemoglobin. Myoglobin is a single polypeptide chain and has a higher affinity for dioxygen than hemoglobin.
The α and β chains of hemoglobin are similar to that of myoglobin, which is unexpected since only 24 of 141 residues in the α and β chains of Hb are identical to amino acids in myoglobin. This suggests that different sequences can fold to similar structures. The globin fold of myoglobin and each chain of hemoglobin is common to vertebrates and must be nature's design for dioxygen carriers. A comparison of the sequence of hemoglobin from 60 species shows much variability of amino acids, with only 9 identical amino founds. These must be important for structure/function. All internal changes are conservative (e.g. changing a nonpolar for a nonpolar amino acid). Not even prolines are conserved, suggesting there are different ways to break helices. The two active site histidines are conserved, as is glycine B6 (required for a reverse turn). http://www.umass.edu/molvis/tutorials/hemoglobin/
Normal and Cooperative Binding of Dioxygen - Structural Analyses
Plots of Y (fractional saturation) vs L (pO2) are hyperbolic for Mb, but sigmoidal for Hb, suggesting cooperative binding of oxygen to Hb (binding of the first oxygen facilitates binding of second, etc). Figure \(\PageIndex{11}\) shows fractional saturation (Y) binding curves vs dioxygen concentration (PO2) for both myoglobin and hemoglobin.
Note that hemoglobin is saturated with O2 at the high concentration found in the lung, but it releases much of its bound O2 in respiring tissues in which O2 is much lower. In contrast, myoglobin only releases significant bound oxygen at much lower O2 concentrations. Hence myoglobin is designed for dioxygen storage.
In another difference, the affinity of Hb for dioxygen, but not Mb, depends on pH. This is called the Bohr effect, after the father of Niels Bohr, who discovered it. Figure \(\PageIndex{12}\) shows binding curves for hemoglobin in the presence of increasing and decreasing concentrations of H+ (pH) as well as for CO2 and another ligand, 2,3-disphosphoglycerate (2,3-DPG).
Michał Komorniczak (Poland). https://commons.wikimedia.org/wiki/F...ohr_Effect.svgCreative Commons 3.0. Attribution-ShareAlike (CC BY-SA 3.0).
Protons (decreasing pH), carbon dioxide, and bisphosphoglycerate, all allosteric ligands which bind distal to the oxygen binding sites on the heme, shift the binding curves of Hb for oxygen to the right, lowering the apparent affinity of Hb for oxygen. The same effects do not occur for Mb. These ligands regulate the binding of dioxygen to Hb.
From these clues, we wish to discern the
- molecular and mathematical bases for the sigmoidal binding curves
- mechanism for the exquisite regulation of O2 binding by allosteric ligands.
The two obvious features that differ between Mb and Hb are the tetrameric nature of Hb and its multiple (4) binding sites for oxygen. Regulation of dioxygen binding is associated with conformational changes in hemoglobin.
Based on crystallographic structures, two main conformational states appear to exist for Hb, the deoxy (or T - taut) state, and the oxy (or R -relaxed) state. The major shift in conformation occurs at the alpha-beta interface, where contacts with helices C and G and the FG corner are shifted on oxygenation. Figure \(\PageIndex{13}\) shows conformation changes on O2 binding to deoxy-hemoglobin (files aligned with DeepView, displayed with Pymol). Dioxygen is shown as red spheres.
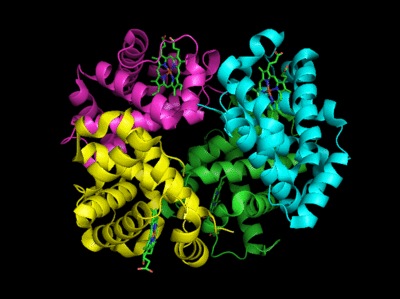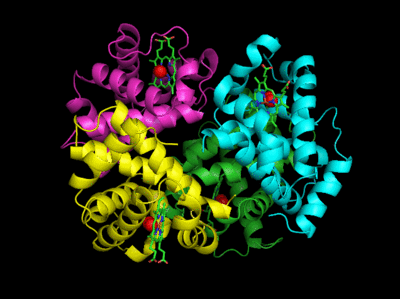
The deoxy or T form is stabilized by 8 salt bridges which are broken in the transition to the oxy or R state. This is Illustrated in Figure \(\PageIndex{14}\).
6 of the salt bridges are between different subunits (as expected from the above analysis), with 4 of those involving the C- or N- terminus.
In addition, crucial H-bonds between Tyr 140 (alpha chain) or 145 (on the beta chain) and the carbonyl O of Val 93 (alpha chain) or 98 (beta chain) are broken. Crystal structures of oxy and deoxy Hb show that the major conformational shift occurs at the interface between the α and subunits. When the heme Fe binds oxygen it is pulled into the plan of the heme ring, a shift of about 0.2 nm. This small shift leads to larger conformational changes since the subunits are packed so tightly that compensatory changes in their arrangement must occur. The proximal His (coordinated to the Fe2+) is pulled toward the heme, which causes the F helix to shift, causing a change in the FG corner (the sequence separating the F and G helices) at the alpha-beta interface as well as the C and G helices at the interface, which all slide past each other to the oxy-or R conformation.
Decreasing pH shifts the oxygen binding curves to the right (to decreased oxygen affinity). Increased [proton] will cause protonation of basic side chains. In the pH range for the Bohr effect, the most likely side chain to get protonated is His (pKa around 6), which then becomes charged. The most likely candidate for protonation is His 146 (on the β chain - HC3), which can form a salt bridge with Asp 94 of the β(FG1) chain. This salt bridge stabilizes the positive charge on the His and raises its pKa compared to the oxyHb state. Carbon dioxide binds covalently to the N-terminus to form a negatively-charge carbamate, which forms a salt bridge with Arg 141 on the alpha chain. Bisphosphoglycerate (BPG), a strongly negatively charged ligand, binds in a pocket lined with Lys 82, His 2, and His 143 (all on the beta chain). It fits into a cavity between the β subunits of the Hb tetramer in the T state. Notice all these allosteric effectors lead to the formation of more salt bridges which stabilize the T or deoxy state. The central cavity where BPG binds between the β subunits becomes much smaller on oxygen binding and the shift to the oxy or R state. Hence BPG is extruded from the cavity.
The binding of H+ and CO2 help shift the equilibrium to the deoxyHb form, which facilitates the release of oxygen to the tissues. It is in respiring tissues that CO2 and H+ levels are high. CO2 is produced from oxidation of glucose through glycolysis and the Krebs cycle. In addition, high levels of CO2 increase H+ levels through the following equilibrium:
\begin{equation}
\mathrm{H}_{2} \mathrm{O}+\mathrm{CO}_{2} \leftrightarrow \mathrm{H}_{2} \mathrm{CO}_{3} \leftrightarrow \mathrm{H}^{+}+\mathrm{HCO}_{3}{ }^{-}
\end{equation}
In addition, H+ increases from weak acids such as pyruvic acid produced in the central metabolic pathway (glycolysis) to produce energy from glucose oxidation.
The binding of CO2 and H+ to hemogl serves an additional function: it removes excess CO2 and H+ from the tissues where they build up. When deoxyHb with bound H+ and CO2 reaches the lungs, they leave as O2 builds and deoxyHb is converted to oxyHb.
Hemoglobin exhibits allosterism. Allosterism occurs when a regulatory ligand (like CO2 and H+) binds to a site distal to the binding site of a main ligand (like O2) and changes the affinity for the main ligand. We will define in our own convention two kinds of allosterism:
Type I occurs when a ligand such as dioxygen binds to multiple ligand binding sites on the same protein and gives sigmoidal binding plot as a function of ligand concentration. Multiple binding sites for a main ligand can be found on a multimeric protein with identical or similar subunits (as in the case of hemoglobin but not myoglobin). In the case of hemoglobin, the main ligand O2 binds to the same active site in each monomer. This site is called the orthosteric binding site. For the hemoglobin tetramer, the orthosteric site of course is the heme Fe2+ ion. Type I allosterism occurs when an allosteric ligand binds at the active sites of the monomeric subunits of the protein. Most texts call this homotropic allosterism and the ligands homotropic ligands. Hence O2 and CO are homotropic ligands for hemoglobin.
Type II occurs when a chemical modulator binds to a site different from the binding site for the main ligand. In doing so, it modulates (activates or inhibits) the binding affinity of the main ligand for the active or orthosteric site and shifts the binding curve for ligand binding. In addition, binding plots at a fixed main ligand concentration with varying modulator concentrations are also sigmoidal. The modulator binds at an allosteric (other) binding site. In the case of hemoglobin, the allosteric modulators are H+, CO2 and BPG. H+ and CO2 binding shift the O2 bind curve in ways that lower the affinity for O2, leading to its release. Most texts call this type of allosterism heterotropic. Protons (H+) and CO2 hence are heterotropic ligands. We prefer Type I and Type II over the more jargonistic less intuitive terms homo- and heterotropic.
Mathematical Analysis of Cooperative Binding
How do the sigmoidal dioxygen binding curves for Hb arise? Mathematics can offer clues that complement and extend structural information. At least three models (Hill, MWC, and KNF) have been developed that give rise to sigmoidal binding curves. Remember, sigmoidal curves imply cooperative binding of oxygen to hemoglobin. As oxygen binds, the next oxygen seems to bind with higher affinity (lower KD). We will discuss the mathematics behind two of the models. Both models are routinely applied to binding phenomena that give sigmoidal curves.
Previously we have shown that the binding of oxygen to myoglobin can be described by chemical and mathematical equations.
\begin{equation}
\mathrm{M}+\mathrm{L} \leftrightarrow \mathrm{ML}
\end{equation}
\begin{equation}
Y=\frac{L}{K_D+L}
\end{equation}
These mathematical equations are that of a hyperbola where Y is fractional saturation. Let's now explore two models that give sigmoidal curves.
Hill Model
In this model, we base our mathematical analysis on the fact that the stoichiometry of binding is not 1:1, but rather 4 to 1: Perhaps a more useful equation to express the equilibrium would be M + 4L ↔ ML4. We can derive an equation analogous to the one above:
\begin{equation}
Y=\frac{L^4}{K_D+L^4}
\end{equation}
For any given L and KD, a corresponding Y can be calculated. A plot of Y vs L is not hyperbolic but sigmoidal (see the next link below). Hence we're getting closer to modeling that actual data. However, there is one problem. This sigmoidal curve does not give a great fit to the actual oxygen binding curve for Hb. Maybe a better fit can be achieved by altering the exponents in the equation. A more general equation for binding might be M + nL ↔ MLn, which gives the Hill equation:
\begin{equation}
Y=\frac{L^n}{K_D+L^n}
\end{equation}
Some books/sources offer a different Hill equation. The one above is correct. Click the derivation below, which requires only a background from the preceding chapter sections and maybe a bit from Chapter 6.1.
- Derivation
-
Let's consider this reaction:
For a minute, assume n=2, and the reaction was written as M + 2L ↔ ML2. Also assume that the reaction occurs when M, L, and a second L all collide simultaneously (unlikely) to form the product, ML2. From introductory chemistry, you would write the rate equation for just the forward "ternary" reaction as:
ratef = d[ML2]/dt = kf[M][L][L] = kf[M][L]2
The rate of just the reverse reaction would be:
rater = d[ML2]/dt = kr[ML2]
Subtract the two rates to get the net rate. Now let's switch from n= 2 back to just n and proceed without further explanation.
At equilibrium, the forward and reverse rates are equal, so
\begin{equation}
\frac{d\left[M L_n\right]}{d t}=k_f[M][L]^n=k_f[M][L]^n-k_r\left[M L_n\right]=0 \text { at equilibrium }
\end{equation}KD is equal to the ratio of kr/kf, so solving for KD gives
\begin{equation}
K_D=\frac{k_r}{k_f}=\frac{[M][L]^n}{\left[M L_n\right]}
\end{equation}Solve for [MLn] gives
\begin{equation}
\left[M L_n\right]=\frac{[M][L]^n}{K_D}
\end{equation}The fractional saturation is given by
\begin{equation}
Y=\frac{\left[M L_n\right]}{[M]+\left[M L_n\right]}
\end{equation}Plug in the previous equation for [MLn] to obtain the correct form of the Hill Equation.
\begin{equation}
Y=\frac{\frac{[M][L]^n}{K_D}}{[M]+\frac{[M][L]^n}{K_D}}\left(\frac{K_D}{K_D}\right)=\frac{[M][L]^n}{K_D[M]+[M][L]^n}=\frac{[L]^n}{K_D+[L]^n}
\end{equation}QED!
If n is set to 2.8, the theoretical curve of Y vs L gives the best, but still not perfect, fit to the experimental data. It must seem arbitrary to change the exponent which seems to reflect the stoichiometry of binding. What molecular interpretation could you give to 2.8?
Consider another meaning of the equilibrium described above: M + 4L ↔ ML4.
One interpretation is that all 4 oxygens bind at once to Hb. Or, alternatively, the first one binds with some low affinity, which through associated conformational changes alters the remaining 3 sites to very high affinity sites. This model implies what is described as infinitely cooperative binding of oxygen.
(Notice that the Hill equation becomes: Y = L/[KD + L], when n =1 (as in the case with myoglobin, and in any equilibrium expression of the form M+L↔ML. Remember plots of ML vs L or Y vs L gives hyperbolas, with KD = L at Y = 0.5.)
Does KD = L at Y = 0.5? The oxygen concentration at which Y = 0.5 is defined as P50. We can substitute this value into equation 3 which gives an operational definition of KD in terms of P50.
\begin{equation}
\mathrm{Y}=0.5=\frac{\mathrm{P}_{50}^{\mathrm{n}}}{\mathrm{K}_{\mathrm{D}}+\mathrm{P}_{50}^{\mathrm{n}}}
\end{equation}
multiply both sides by 2 give
\begin{equation}
\begin{gathered}
1=\frac{2 \mathrm{P}_{50}^{\mathrm{n}}}{\mathrm{K}_{\mathrm{D}}+\mathrm{P}_{50}^{\mathrm{n}}} \\
\mathrm{K}_{\mathrm{D}}+\mathrm{P}_{50}^{\mathrm{n}}=2 \mathrm{P}_{50}^{\mathrm{n}} \\
\mathrm{K}_{\mathrm{D}}=\mathrm{P}_{50}^{\mathrm{n}}
\end{gathered}
\end{equation}
Note that for this equation, KD is not the ligand concentration at half-saturation as we saw in the case with hyperbolic binding curves.
This gives a modified version of the Hill equation for hemoglobin binding of dioxygen:
\begin{equation}
Y=\frac{L^n}{P_{50}^n+L^n}
\end{equation}
This Hill equation with the Hill coefficient n that is empirically determined to obtain the best fit to the binding data might seems a bit contrived (especially after seeing the more mechanistically and chemically intuitive MWC equation described below). Is it useful in any other circumstance? Indeed it is and it is used often in modeling more complex interconnected binding and kinetic pathways that show similar "exquisite" sensitivity to concentrations and resulting sigmoidal binding and kinetic plots. We will see its use in Chapter 30.13 when we model protein kinases that regulate the cell cycle!
Use the sliders in the interactive graph below to explore the effect of changes in KD and n on fractional saturation.
The Hill equation for hemoglobin gives sigmoidal dioxygen binding curve that fit the actual binding data.
MWC Symmetry Model
In the MWC (Monod, Wyman, and Changeux) model, in the absence of ligand (oxygen), hemoglobin is assumed to exist in two distinct conformations, the T state (equivalent to the crystal structure of deoxyHb) and the R state (equivalent to the crystal structure of oxyHb without the oxygen). In the absence of dioxygen, the T state (T0) is greatly favored over the unliganded R state (R0) at equilibrium. In the presence of increasing oxygen, the R state is favored.
A constant (somewhat equivalent to a dissociation constant) can be defined.
\begin{equation}
\mathrm{L}=\mathrm{T}_{0} / \mathrm{R}_{0}
\end{equation}
(Note: L is not the ligand concentration so don't get confused.) In addition, let us assume that hemoglobin can not exist with some of the monomers in the tetramer in the T state while others in the same tetramer are in the R state. Hence this model is often called the symmetry model. Finally, let's assume that each oxygen can bind to either the T or R state with the dissociation constants KT and KR respectively. These constants do not depend on the number of dioxygens already bound to the tetramer. Hence
\begin{equation}
\mathrm{K}_{\mathrm{R}}=\frac{\left[\mathrm{R}_{0}\right][\mathrm{S}]}{\left[\mathrm{R}_{1}\right]}=\frac{\left[\mathrm{R}_{1}\right][\mathrm{S}]}{\left[\mathrm{R}_{2}\right]}=\ldots \frac{\left[\mathrm{R}_{\mathrm{n}}\right][\mathrm{S}]}{\left[\mathrm{R}_{\mathrm{n}+1}\right]}
\end{equation}
and
\begin{equation}
\mathrm{K}_{\mathrm{T}}=\frac{\left[\mathrm{T}_{0}\right][\mathrm{S}]}{\left[\mathrm{T}_{1}\right]}=\frac{\left[\mathrm{T}_{1}\right][\mathrm{S}]}{\left[\mathrm{T}_{2}\right]}=\ldots \frac{\left[\mathrm{T}_{\mathrm{n}}\right][\mathrm{S}]}{\left[\mathrm{T}_{\mathrm{n}+1}\right]}
\end{equation}
where the subscript on R and T refers to the number of dioxygens bound to that form of R or T. A cartoon representation of the T and R forms and accompanying dioxygen binding is shown in Figure \(\PageIndex{15}\).
Now define two new parameters:
\begin{equation}
\alpha=\frac{\mathrm{pO}_{2}}{\mathrm{~K}_{\mathrm{R}}}=\frac{[\mathrm{S}]}{\mathrm{K}_{\mathrm{R}}}
\end{equation}
where α is really a normalized ligand concentration describing how many times the KR the ligand concentration is, and
\begin{equation}
\mathrm{c}=\frac{\mathrm{K}_{\mathrm{R}}}{\mathrm{K}_{\mathrm{T}}}
\end{equation}
the ratio of the dissociation constants for the R and T forms.
If oxygen binds preferentially to the R form of hemoglobin, c would be a small fractional number. In the limiting case, when oxygen didn't bind to the T form, KT would be infinite, and c = 0.
Using these definitions and equations, the following equation for Y, fractional saturation vs α can be derived, with n, the number of binding sites per molecule, = 4 for Hb.
\begin{equation}
\mathrm{Y}=\frac{\alpha(1-\alpha)^{\mathrm{n}-1}+\operatorname{Lc} \alpha(1+\mathrm{c} \alpha)^{\mathrm{n}-1}}{(1+\alpha)^{\mathrm{n}}+\mathrm{L}(1+\mathrm{c} \alpha)^{\mathrm{n}}}
\end{equation}
Figure \(\PageIndex{16}\) shows how fractional saturation (Y) vs alpha varies with L and c for the MWC model.
When L is set at 9000 and c = 0.014, the Y vs α curve fits the experimental oxygen binding data well. Figure \(\PageIndex{17}\) shows the best experimental dioxygen binding data that we could find (obtained from a graph, not from a table), the best fit of the Y vs L data using a Hill coefficient of n=2.8 (fitting equation 3 above), and the best fit of Y vs L using the MWC model, with L=9000, c=0.014, and Kr = 2.8 torr.
Use the sliders in the interactive graph below to explore the effect of changes in L and c on fractional saturation.
Hence, like the Hill equation, the MWC equation gives sigmoidal dioxygen binding curves. It does not require an empirical Hill-like coefficient, which has no clear physical meaning!
Another way to think about the MWC Model
The MWC model assumes that oxygen binds to either the T or R form of Hb in a noncooperative fashion. Hence KT and KR are constant, independent of the number of dioxygens bound to that form. If so, what is the basis of the cooperative oxygen binding curves? The answer can be seen below. The cyan curve might reflect the binding of a ligand to the T form of a macromolecule, with KD = 100 uM (low affinity), for example. The binding curve looks linear, but it really is just the initial part of a hyperbolic binding cure. Likewise, the magenta curve reflects the binding of a ligand to the R form of the macromolecule with KD = 10 uM. The T and R forms are linked through the T↔ R equilibrium. That equilibrium will be shifted to the tighter binding (lower KD) R form with increasing ligand concentration, assuming the ligand binds preferentially to the R form. This shifts the actual binding curve from that resembling the T form at low ligand (cyan) to one resembling the R form (magenta) as the ligand increases, imparting sigmoidal characteristics to the "observed" binding curve (gray). Figure \(\PageIndex{18}\) shows how sigmoidal binding curve could arise from a switch from a low affinity to high affinity form.
KNF Sequential Model
The KNF (Koshland, Nemethy, and Filmer) Sequential model was developed to address concerns with the concerted model. One of the major problems with the concerted model is that it seemed unrealistic to expect all the subunits to change conformation together. Why shouldn't there be some differences in subunit conformation? The KNF model also fits the experimental data well. Figure \(\PageIndex{19}\) shows the linked equilibria in the KNF model. Data suggests that the MWC model better explains the transition in proteins on ligand binding and that there is an all‑or‑none interconversion between the two states.
Allosterism in other multisubunit protein complexes
Changeux (of the MWC model) has written eloquently about the occurrence and effects of allostery in other proteins. We will encounter these proteins in other chapters, but present some here, in advance of the chapter in which they are usually discussed. We do this to show that other proteins display allostery and that the MWC can often be used in describing their behaviors. This offers a rationale to discuss allosterism using hemoglobin with its nonstandard covalent ligands as a model for allosteric binding proteins and enzymes.
Environmental factors such as ligands and allosteric modulators can shift the degree of cooperativity for ligand binding, promote allosteric rearrangements and T ↔ R transitions of proteins other than hemoglobin. We offer several examples of multimeric proteins (complexes) that display allosterism. Many of these allosteric proteins not only bind ligands, but acts as catalysts. One protein, a ligand-gated ion channel, moves ions across a membrane. Others catalyze the chemical transformation of a substrate to a product. Another is a structural viral protein. The examples involving catalysis are more complex, since an additional step (transport of ions or alteration in covalent bonds) after binding is added to effect protein function. This extra step can be described as a rate, so we explore rate vs ligand concentration, not just fractional saturation vs ligand concentration curves.
Lactate dehydrogenase (LDH)
LDH is an enzyme that catalyzes the reversible reduction of the 3-carbon carboxylic acid pyruvate to lactate by the oxidizing agent NAD+, as shown in the reaction below (which is written in reverse as the reduction of pyruvate, the normal function of the enzyme).
pyruvate + NADH + H+ ↔ lactate + NAD+
Its activity is modulated by the allosteric activator fructose 1,6-bisphosphate (FBP). The kinetics can be modeled using the MWC model, in which the enzyme exists in T (tense/taut) and R (relaxed) allosteric states. FBP binds preferentially to the R state.
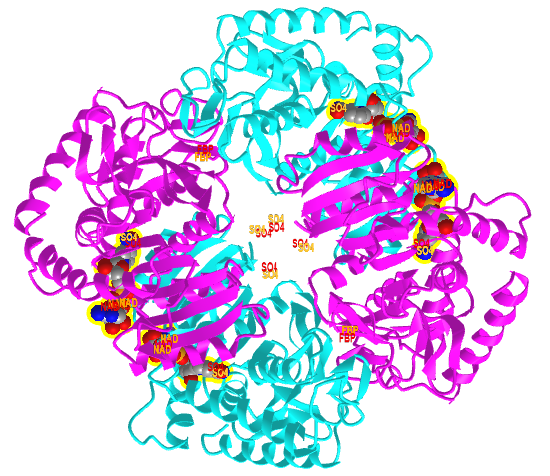
Figure \(\PageIndex{20}\) shows an interactive iCn3D model comparing the T state of bacterial L-lactate dehydrogenase with bound NAD+ from Bifidobacterium longum (1LLD), and the R state of the enzyme from Geobacillus stearothermophilus (2LDB) with bound NAD+ and the allosteric activator fructose 1,6-bisphosphate (F6P). Toggle between the two states using the "a" key.
Figure \(\PageIndex{20}\): Comparison of the T (1LLD) and R (2LDB) states of bacterial L-lactate dehydrogenase with bound NAD+ and allosteric activator F6P (in R state) (Copyright; author via source). Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...YEXKSp5J1ErFT6
The enzyme substrate NAD+, the allosteric activator F6P for the R state, and SO42- (from ammonium sulfate used to crystallize the protein) are shown in spacefill and labeled.
Aspartate transcarbamylase (ATCase)
This enzyme catalyzes the addition of aspartate and carbamoyl phosphate to form carbamoyl aspartate, the first step in the pathway for the synthesis of the pyrimidine nucleotides cytidine triphosphate (CTP) and uridine triphosphate (UTP).
The end products of the pathway, CTP and UTP, feedback and allosterically inhibit the enzyme. In contrast, ATP is an allosteric activator. This prevents a buildup of pyrimidine nucleotides over purine nucleotides since equal amounts are needed for nucleic acid synthesis.
Figure \(\PageIndex{21}\) shows an interactive iCn3D model comparing the T (4FYW) and R (1D09) states of asparatate transcarbamylase (ATCase). Toggle between the two states using the "a" key.
Figure \(\PageIndex{21}\): Comparison of the T tense (4FYW) and R (1D09) relaxed state of asparatate transcarbamylase (ATCase). Toggle between the two states using the "a" key. (Copyright; author via source). Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...MHLtC9ALwWVia6
Each of the subunits is shown in a different color. The T state (4FYW) has bound CTPs (at the periphery, shown in spacefill) while the R state has a bound substrate analog, N-(phosphonacetyl)-L-aspartic acid. High levels of the substrate (or substrate analog) shifts the equilibrium to the active R state.
Pentameric ligand-gated ion channels (bacterial)
Protein channels in membrane bilayers are needed to "catalyze" and regulate the flow of ions across the hydrophobic membrane. Hence it makes sense that channels exist in closed and open states. One example is the bacterial GLIC pentameric ligand-gated ion channel, which is opened by ligand binding, often called ligand-gating..
Figure \(\PageIndex{22}\) shows an interactive iCn3D model comparing the GLIC pentameric Ligand-Gated Ion Channel Loop2-22' oxidized mutant in a locally-closed conformation (LC3 subtype) (3TLV) and the A237F mutant channel in the open conformation (3LSV). Toggle between the two states using the "a" key.
Figure \(\PageIndex{22}\): Comparison of the GLIC pentameric Ligand-Gated Ion Channel Loop2-22' oxidized mutant in a locally-closed conformation (LC3 subtype) (3TLV) and the A237F mutant of the pentameric ligand gated ion channel from Gloeobacter Violaceus in the open conformation (3LSV). Toggle between the two states using the "a" key. (Copyright; author via source). Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...GKiPY9Jh7tQXTA
Note that the outer (red) and inner (blue) membrane leaflets are shown only in the closed channel (3TLV). The green spheres represent chloride ions.
Nudaurelia capensis ω virus capsid
This hallow viral protein structure surrounds the internal viral genome, so it is an example of allostery in a protein complex that is neither a transporter nor an enzyme. This hetero 480-mer with icosahedral symmetry undergoes a global shape change when the immature capsid undergoes selective and limited proteolysis to form the mature capsid, as illustrated in Figure \(\PageIndex{22}\).

The R form is more open. This is a wonderful example to envision the global conversion of all subunits from a "T" to an "R" state, clearly necessary in this case to preserve the exquisite symmetry!
Now, let's look at binding and rate curves for some multimeric allosteric enzymes. Since this is all a bit complicated, let's review again the difference between what we call Type 1 and Type II allosterism:
Type I: Increasing the amount of a substrate can induce conformational changes in a multisubunit protein to a form that has apparently higher (or potentially lower as well) affinity for the substrate in the remaining unoccupied substrate binding sites. In this case, the substrate is binding to the orthosteric site. These sites are where substrates bind but also competitive inhibitors (if the protein is an enzyme), and agonists or competitive antagonists of receptors. We will explore enzymes and receptors later in this book. In Type I allosterism, binding or kinetic curves would show sigmoidal fractional saturation (or kinetic curves) with increasing concentrations of substrate.
Type II: Increasing amounts of a chemical species (an inhibitor or activator) can bind to an allosteric site, which affects the binding of the substrate to the orthosteric site. The regulators shift and change the shape of the Y or rate curves vs substrate. In experiments to show this kind of allosterism, you wouldn't change the substrate and allosteric effector concentrations simultaneously since the resulting data and graphs would be hard to interpret. You could change the ligand or substrate that binds to the orthosteric site over a large range of concentrations (hopefully over a 1000 - 10,000 fold change, or 4 log units) in several different experiments, with each experiment having a different fixed concentration of the allosteric effector. Alternatively, you could conduct the experiment over a large concentration range of a given allosteric effector (again a 1000-10,000 fold change if possible) in several different fixed concentrations of ligand or substrate in a series of experiments.
Rate vs ligand curves for allosteric proteins that catalyze chemical reactions
Since we have already seen an example of Type I allosteric binding curves (hemoglobin binding dixoygen), let's look at a few examples of Type II allosteric in multisubunit proteins since their graphs are a bit more complicated. We realize the curves below show relative rates of enzymes and not relative fractional saturation of enzymes, but the same principles are present.
Phosphofructokinase
Figure \(\PageIndex{23}\) shows an example of allosteric kinetic curves for Phosphofructokinases A (Pfk A) and B (Pfk B) from Mycobacterium tuberculosis. The enzyme catalyzes the phosphorylation of fructose-6-phophate (F6P) by ATP to produce fructose-1,6-bisphosphate (F1,6-BP) and ADP.
F6P + ATP → F1,6-BP + ADP
Figure \(\PageIndex{23}\): The dependence of Pfk A and Pfk B activities on concentration of Mg2+. Individual reactions were performed in buffers containing fixed initial concentration for both substrates (1 mM F6P and ATP) with the concentration of Mg2+ varied. Snášel, J. et al. Int. J. Mol. Sci. 2021, 22, 1483. https://doi.org/10.3390/ijms22031483. Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Only Pfk A shows allosteric activation of the enzyme by Mg2+, run under fixed initial (and probably saturating) concentrations of the substrates F6P and ATP. The Hill coefficient is 3.3 for Pfk A, which suggests that Mg2+ is important in maintaining/promoting the active site and formation of the enzyme tetramer. Pfk B shows hyperbolic kinetics and no allosterism, with a Hill coefficient close to 1. These curves are modeled with the Hill equation and not the MWC equation.
Lactate Dehydrogenase
Again this enzyme catalyzes the following reaction:
pyruvate + NADH + H+ ↔ lactate + NAD+
The graphs in Figure \(\PageIndex{24}\) show relative inhibition (graph A, top) and double-reciprocal plots (C, bottom) for the enzyme lactate dehydrogenase B (LDHB) in the presence of an allosteric inhibitor, AXKO0046. This enzyme catalyzes the reduction of pyruvate by NADH (the substrate) to form lactic acid and NAD+ (the products). We'll discuss the graphs below.
Figure \(\PageIndex{24}\): Biochemical characterization of AXKO-0046. LDHB inhibition by AXKO0046 was studied using varying concentrations of (a) NADH (c) Double reciprocal (Lineweaver-Burk) plots of the kinetic data. Shibata, S. et al. Sci Rep 11, 21353 (2021). https://doi.org/10.1038/s41598-021-00820-7. Creative Commons Attribution 4.0 International License. http://creativecommons.org/licenses/by/4.0/.
Now, these graphs are a bit more complicated since in this case, the initial concentration of one substrate is varied, while the other concentration is fixed (in contrast to the PfkA experiments in which the initial concentrations of both substrates were held constant).
Let's look at graph C (bottom) first. Instead of showing graphs of rate vs [NADH], the authors showed double-reciprocal kinetic plots, run with varying [NADH] and at one fixed concentration of pyruvate (not given) and several fixed concentrations of inhibitor. The graphs look like they are generally straight lines except at the end, which occurs at a low concentration of NADH (which gives the highest value of 1/[NADH] = 0.10). At this point, 1/rate (given as 1/v) data points are higher than the best-fit line would suggest, implying that the rate v is "abnormally" low. That rate accelerates as [NADH] increases (as 1/[NADH] decreases in a manner consistent with allosterism. This suggests that at any given fixed concentration of inhibitor and fixed pyruvate concentration, the graphs of rate vs substrate (NADH) (i.e not the double-reciprocal plot) would be sigmoidal. It's different from the graph for PfkA (Fig 23), in which the x-axis variable is the allosteric activator Mg2+.
Look at Graph A (top) which uses varying inhibitor concentrations and several different fixed concentrations of reactant NADH. This is analogous to the graph for PfkA but notice that on the x-axis the log [inhibitor] is plotted instead of the [inhibitor]. These are NOT plots of v vs [substrate], expected to be hyperbolic, or v vs log[substrate] which are expected to be sigmoidal. (A lesson here is to look carefully at the axes). But note something unusual about the curves. The plateau for inhibition is not the same at each NADH concentration. The highest % inhibition (red and purple curves) occurs when the substrate [NADH] is highest. (We will see in the next chapter that this is a sign of what is called uncompetitive inhibition).
X-ray crystal structures show that the inhibitor (AXKO-0046) does bind to an allosteric site, not the active orthosteric site. It appears to bind in the interface of the LDHB tetramer. The graphs show that over four orders of magnitude of inhibitor (4 log units), the inhibition goes from 0 to about 100%, which is expected if the sigmoidal semi-log curves gave hyperbolic curves with [inhibitor] plotted on the x-axis.
This may seem confusing, but such sigmoidal curves are found in plots of rate vs log concentration of allosteric activators and inhibitors, as discussed in Chapter 5.1. So don't immediately jump to the conclusion that a sigmoidal curve implies allosterism. Look at the reactions and relative concentrations carefully.
Consider this example. What if a protein binds a ligand L and an inhibitor I at the same orthosteric site? If one bound, the other couldn't. This is an example of a classical competitive, non-allosteric, inhibition. Now, what if an inhibitor, I, binds to an allosteric site and when bound, it altered the conformation of the orthosteric site such that the ligand could not bind. Binding of L and I would be mutually exclusive. This would produce the same binding curves as the classical competitive inhibition. In either case, at very high ligand concentrations, the effect of the inhibitor would be lost, and full maximal binding would be observed. It would just take higher concentrations of ligand to get the same fractional saturation of the protein in the presence of the inhibitor than in its absence. In the presence of a fixed concentration of these competitive inhibitors, the effective KD would be higher. Y vs L curves for both would be hyperbolic, and double-reciprocal plots would be linear.
Allostery within monomeric protein
Allosterism can also occur in monomeric proteins:
Type I (again our nomenclature) allosterism can occur in monomers that have more 2 or more binding sites for a ligand/substrate and if the binding of ligand/substrate to one site significantly alters the affinity of the other site for substrate enough to produce a nonhyperbolic, sigmoidal binding/kinetic curve for substrates. This case is different than the binding of substrate to two different preformed substrate binding sites, each with a different fixed affinity, which we discussed in Chapter 5.1 (scroll down to binding of a ligand to two independent sites). We show again the graph of fractional saturation Y vs L for the binding of a ligand to two different preformed sites of different affinities below.
Note that the above graph doesn't look sigmoidal. It is essentially hyperbolic except in the extreme case when one of the KD is much much less than the other AND at low ligand concentration such that the higher affinity binding leads to an abrupt, titration curve-like saturation of the low KD site before the second site has much occupancy.
Rec A is an OK example of a "possible" Type I allosteric monomer binding protein (if you have a better example, let us know!). This protein is required for homologous recombination in bacteria. It has ATPase activity and catalyzes ATP-driven homologous pairing and strand exchange of DNA required for DNA repair. The structure is known for the Mycolicibacterium smegmatis apo form of the enzyme, the enzyme:substrate (dATP, a substrate analog) complex, and the enzyme:substrate:allosteric effector (a second dATP and possibly citrate) complex.
The enzyme has three domains (N-terminal 1-30, the major M domain (31-269) and the C-terminal (270-349). The M domain is the catalytic domain which has nucleotide triphosphate hydrolase activity. It binds nucleotides, DNA and also interacts with the N domain of another RecA to promote the polymerization of RecA into a filament. The C-terminal domain is disordered but becomes ordered when bound to a second dATP in the crystal structure.
Figure \(\PageIndex{25}\) shows conformational changes in RecA:dATP (the ES complex) on binding a second dATP (the ESA complex), where A is the likely allosteric activator (the second bound dATP). A result of this ordering on binding is likely the polymerization of the RecA into filaments.
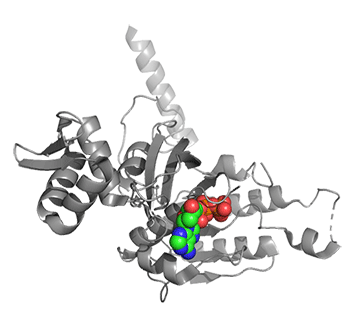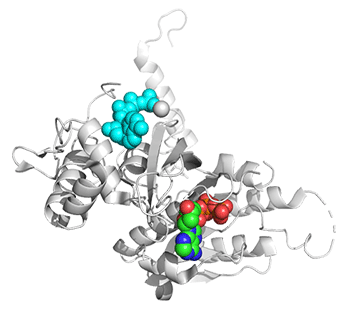
Figure \(\PageIndex{25}\): Conformational changes in RecA:dATP (the ES complex) on binding a second dATP (the ESA complex).
The dATP in the catalytic site is shown in spacefill with CPK colors. The ES complex is shown as a darker gray protein with one bound dATP (spacefill, CPK colors). The ESA complex is shown in lighter gray with dATP bound in the catalytic (orthosteric) site in CPK colors and a second dATP (spacefill, cyan) bound in the putative allosteric site in the C domain.
Type II: increasing amounts of a chemical species (an inhibitor or activator) that binds to an allosteric site in a monomeric protein could affect the binding of the substrate to an orthosteric site in the monomer. In this case, as in Type II for multimeric proteins, you could again run two different types of experiments (one with varying substrate at 3-4 different fixed allosteric effector concentrations or vice/versa.
One example is thrombin, the last protease in a cascade of clotting proteins. The proteins are synthesized as inactive precursors (zymogens) that become activated on limited proteolysis. Active thrombin is a procoagulant enzyme in that it can cleave circulating fibrinogen (and other procoagulant molecules) into fibrin. This then self-associates to form a fibrin clot.
Paradoxically, thrombin also has anticoagulant properties in that it can cleave another circulating protein, Protein C, which e inhibits further clotting. Thrombin does so when it binds a transmembrane protein, thrombomodulin, present on endothelial cells that line blood vessels.
These contrasting activities support the notion that thrombin has two interconverting conformations, each stabilized by different ligands or proteins. One such ligand is the simple monatomic ion Na+. Indeed, thrombin appears to have two main catalytic conformations, a high-activity “fast” form (with bound Na+) and a low-activity “slow” form (without bound Na+). The fast form with bound Na+ (15 Å from the active site) appears to be the procoagulant form while the slow form is the anticoagulant form.
Figure \(\PageIndex{26}\) shows an interactive iCn3D model comparing the anticoagulant slow form of thrombin (1SGI) and the procoagulant sodium-bound fast form of thrombin (1SG8). Toggle between the two states using the "a" key.
Figure \(\PageIndex{26}\): Anticoagulant slow form (1SGI) and the procoagulant sodium-bound fast form of thrombin (1SG8). Toggle between the two states using the "a" key. (Copyright; author via source). Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...kxnATvMdVD1566
The magenta represents the slow form and the cyan with bound Na+ the fast form which has enhanced coagulant activity
Table \(\PageIndex{1}\) below shows a list of monomeric allosteric proteins and their PDB file codes. The proteins (P) are enzymes that bind a substrate (S) and an allosteric effector (A) to form PS, PA, PAS complexes (adapted from Wang et al. J. Phys. Chem. Lett. 2021, 12, 5404−5412)
| protein | P | PA | PS | PAS | Effect |
| protein RecA (RecA) | 2OES | 2ODN | 2G88 | activation | |
| mitogen-activated protein kinase 8 (MAP8) | 1UKH | 3O2M | 2XRW | inhibition | |
| cAMP-dependent protein kinase catalytic. subunit alpha (Prkaca) | 4NTS | 4NTT | 4IAF | inhibition | |
| cAMP-dependent protein kinase catalytic. subunit alpha (Prkaca) | 4NTS | 1BKX | 4DG0 | activation | |
| cyclin-dependent kinase 2 (CDK2) | 3PXR | 3PXF | 1HCK | inhibition | |
| casein kinase II subunit alpha (CK2α) | 5ZN5 | 3H30 | 2PVR | inhibition | |
| myosin-2 heavy chain (mhcA) | 1FMV | 2JJ9 | 2JHR | inhibition | |
| tyrosine-protein phosphatase. nonreceptor type 1 (PTP1B) | 4QBW | 1T49 | 1PTV | inhibition | |
| 1T48 | |||||
| 1T4J | |||||
Hemoglobin variants and disease
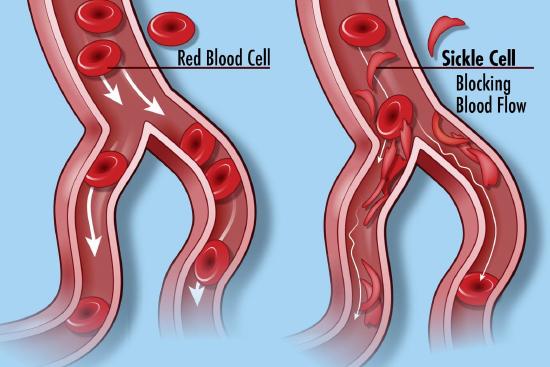
Many diseases have been associated with alternations in the amino acid sequence of hemoglobin. Around 300,000 babies are born each year with a genetic disorder causing an aberrant hemoglobin structure. Over 80% of these are in low/middle-income countries. The worst is sickle cell anemia followed by β-thalassaemias and the less serious α-thalassaemias. We will only focus on sickle cell disease. In this disease, red blood cells become distorted in share from a normal smooth discoid shape to a crescent-like shape under low oxygen concentrations found in capillaries. These impede blood flow as shown in Figure \(\PageIndex{25}\) and lead to symptoms ranging from anemia, episodic pain, swelling of hands and feet, and vision problem. Complications often lead to premature death.
Linus Paul and colleagues showed that the isoelectric point (pI) of oxy-Hb and deoxy-Hb in normal blood was 6.87 and 6.68, respectively, but were higher (7.09 and 6.91, respectively) in sickle cell disease. This was the first evidence that a disease was caused by a molecular alteration of a protein. Eventually, we learned that a single negatively charged amino acid, Glu 6, on the β-chain of hemoglobin was mutated to a nonpolar one, valine. This causes hemoglobin, which is present at a concentration of 150 g/L in blood to self-aggregate into a long polymer. This distorts the cell in a sickle shape. Humans have two genes for the beta chain of hemoglobin, one from the egg donor and the ohter from the sperm donor. If only one mutated, the disease is called sickle cell trait. If both are mutated, sickle cell disease is observed.
The hydrophobic Val 6 in on the surface of both beta chains in sickle cell disease. It can bind to a hydrophobic patch comprised of Ala 70, Phe 85 and Leu 88 on another β-chain on another hemoglobin tetramer. Hence hemoglobin has two Val 6s and two hydrophobic patches, allowing first the formation of a sickle cell hemoglobin "dimer" of tetramers, followed by elongation of the growing fibril. This is a disease of aberrant induced dipole-induced dipole interactions and the "hydrophobic effect".
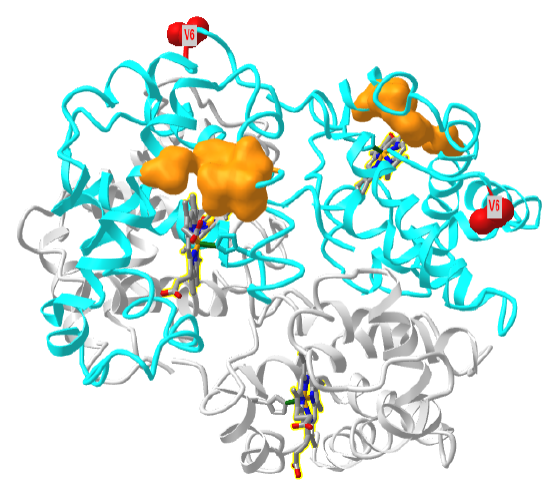
Figure \(\PageIndex{27}\) shows a "dimer" aggregate of two hemoglobin S tetramers, in which each β-chain has the D6V mutation. α chains are shown in grey, β chains in cyan, Val 6 in red spacefill and the surface hydrophobic patch of A70, F85 and L88 in orange spacefill (1hbs). Note the binding of the two tetramers is mediated by the interaction of the red Val 6 on the right tetramer with the orange surface hydrophobic patch on the left tetramer. Note also that there are the "dimer" aggregate has three more exposed Val 6 (red sphere) and three more hydrophobic patches. This would allow the extension of the dimer and the formation of long fibril-like polymers, with binding mediated by noncovalent interactions.
Figure \(\PageIndex{28}\) shows an interactive iCn3D model of one tetramer of hemoglobin S. As in Figure \(\PageIndex{21}\), the α chains are shown in grey, the β chains are shown in cyan, and Val 6s are shown in red spacefill. The surfaces of the hydrophobic pockets where the Val 6 another HbS tetramer binds, comprised of amino acids A70, F85 and L88, are shown in orange.
Sickle cell disease and trait are endemic in Sub-Saharan Africa, where over 4 million have the disease and over 40 million have the trait. Its geographic distribution, along with that of malaria, is shown in Figure \(\PageIndex{29}\).
The Plasmodium parasite reproduces in red bloods cells. Their ability to reproduced is compromised as red blood cells with sickle cell hemoglobin rupture more frequently. Also the parasite uses hemoglobin as a source of amino acids. The endocytose it and hydrolyze it to amino acids in digestive organelles. Sickle cell hemoglobin is more resistant to this process. Hence evolution appears to have maintained the sickle cell gene in these areas as protection against malaria.
Sickle cell disease is a systemic problem, so treatment of the multitude of symptoms is important. Some of these treatments are described in Figure \(\PageIndex{30}\).
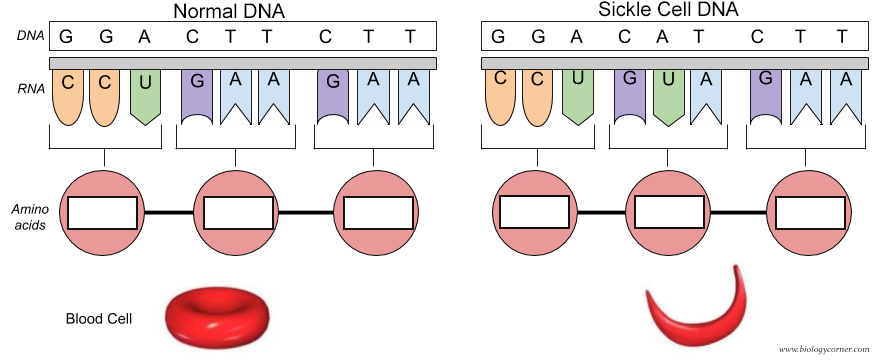
Of course the cure would be to use DNA editing to change the base pair for the mutated Val 6 gene back to the wild-type Glu 6 as shown in Figure \(\PageIndex{31}\). The amino acid sequence encoded by the DNA and RNA shown below is Pro-Glu-Glu for the normal and Pro-Val-Glu for the sickle cell chain.
Crisper gene editing trials are now underway to attempt a cure of this dreadful disease.




oR(1D09)State.png?revision=1&size=bestfit&width=422&height=382)
%25C2%25A0to_the_open_conformation_(3LSV).png?revision=1&size=bestfit&width=288&height=359)
__procoagulant_sodium-bound_fast__thrombin_(1SG8).png?revision=1&size=bestfit&width=228&height=241)