32.12: A Warmer World: Temperature Effects On Proteins

Search Fundamentals of Biochemistry

Inspiration for the chapter comes from Biochemical Adaptation by Hochachka and Somero.

Introduction

 

In the previous chapter section, we discussed the generalized effects of temperature on chemical/biochemical reactions.  The rate for chemical reactions, including enzyme-catalyzed ones, typically increases 2-3 fold (Q₁₀ values) with a 10⁰ C temperature increase over an organism's typical temperature range.  Q₁₀ values decrease at higher temperature pairs differing by 10⁰ C.  At too high a temperature, a protein enzyme destabilizes, and Q₁₀ values can fall to less than 1, a sign of potential trouble for an organism subjected to that higher temperature.  

As we saw in Chapter 32.11 and will here, two competing processes affect protein enzymes as temperatures increase.  They are increased rates for the catalyzed reaction and increased conformational dynamics, which leads to eventual denaturation at high enough temperatures.  Hence evolution would presumably select for increased protein stability for organisms adapted to higher temperatures.  

For cold-adapted organisms, the rates of catalysis are expected to decrease.  Hence evolution might lead to higher k_cat values for cold-adapted organisms.  However, we saw in Chapter 32.11 that the rate-limiting step for enzyme-catalyzed reactions often involved localized conformational changes, which would be disfavored at colder temperatures.  Hence evolution would also select for enzymes that could maintain flexibility at low temperatures.  In Chapter 4.9, we discussed low-temperature protein denaturation.  Proteins can be destabilized at low temperatures.  In this section, we will study how enzymes can adapt to higher temperatures. We won't discuss how proteins adapt to cold since this topic is less relevant for human-caused climate change. 

We will follow the approach used throughout this book - that structure mediates function.  We will use a lot of enzyme kinetics since kinetic parameters can tell us much about how bound substrate goes to product at high substrate concentrations (k_cat or V_M) or low substrate concentrations (k_cat/K_M) at different temperatures and for different orthologs of enzymes from species that have adapted to grow at low (psychrophile), medium (mesophile) or high temperatures (thermophiles).  We'll next look at the structure of enzymes and which features allow them to adapt to their optimal temperature for growth.  Finally, we will look at entire pathways to discern clues as to how they adapt to increased temperatures. 

 

An Overview - Soil Enzymes

Soil microbes play a key part in the carbon cycle as they can both store and release carbon.  Soil temperatures influence this balance between uptake and release of CO₂ into the atmosphere.  

Soil Organic Carbon - SOC

The soil is a sink for carbon and stores about 1500 gigatons [Gt] = 1.5 Pt = 1500 Pg), more than the atmosphere and vegetation combined. SOC derives ultimately from photosynthetic organisms.  When they die, their carbon is used by heterotrophs for energy and biosynthesis. Carbon can also be returned to the atmosphere by aerobic oxidation by microorganisms, but this requires O_2, which diminishes rapidly with soil dept. Oxygen levels depend on soil porosity, relative amounts of sand and clay, and hydration.  Tilling of soil increases O₂ exposure and hence oxidative respiration of SOC, increasing atmospheric CO₂.  No-till farming hence can decrease CO₂ release into the atmosphere.  Inorganic carbon from CO₂ (HCO₃⁻, and CO₃^-2) bind with cations in the soil (mineralization) or is released into the atmosphere as CO₂.

Carbon input into the soil is mostly determined by photosynthesis, which correlates with root mass, and decay, while export is determined by soil microbial (bacteria, fungi, protists, animals) respiration.  Microorganisms play a key role in the balance of carbon input and release in the soil and hence are prime determinants of SOC.  

SOC is high in northern latitudes since colder temperatures promote lower respiration rates and accumulation of SOC over time.  SOC is low in the lush tropics (even given the high photosynthetic rates) because of a high microbial respiration rate at higher temperatures.  Deforestation of the lush Amazon Rain Forest will leave soil poor SOC with little to balance CO₂ release from the decomposition of what's left by the abundant soil microorganisms.

About 21 Gt of the 1500 Gt of SOC consists of microbial mass (12 Gt fungi, 7 Gt bacteria and 2 Gt from animals).  Fungi hence are key players in soil metabolism. They are involved in the slow decomposition of decaying organic matter and promote the growth of slow-growing organisms like trees.  In contrast, bacteria are fast metabolizers, and are found in abundance in grasslands.  Northern attitudes have a higher soil microbial mass than in the tropics, but they are less active, allowing great SOC stores. 

We often think of enzymes working in an aqueous environment in a test tube or a cell (which is very crowded with other molecules).   Figure \(\PageIndex{1}\) below represents the microenvironment of soil enzymes involved in the decomposition of SOC, like cellulose.

Figure \(\PageIndex{1}\): Location of enzymes in soils and their importance for carbon and nutrient cycling.  Fanin, N. et al. (2022). Soil enzymes in response to climate warming: Mechanisms and feedbacks. Functional Ecology, 36, 1378– 1395. https://doi.org/10.1111/1365-2435.14027.  Permission from John Wiley and Sons and Copyright Clearance Center.

Figure \(\PageIndex{2}\) below give a review and an overview of the effects of increasing temperature on soil enzymes.

Figure \(\PageIndex{2}\): Effects of temperature at the enzyme scale.  Fanin, N. et al., ibid.  Permission from John Wiley and Sons and Copyright Clearance Center.

Panel (a) shows the many steps involved in enzyme catalysis that can be affected by temperature changes.    Step 1 shows the binding of substrates.  The K_M (units M) for the enzyme gives a "measure" of the strength of the interaction (but remember that K_M = K_D - the dissociation constant - only under rapid equilibrium conditions).  Step 2 reflects k_cat, the "net" rate constant for converting bound substrate to product.  

Panel (b) shows how key constants change with increasing temperature.  The figure shows that k_cat increases with temperature, consistent with the Arrhenius equation, as the temperature coefficient Q₁₀ decreases (as discussed in Chapter 12.11).  (Remember that Q10 is the factor by which the reaction rate, k or R, changes for each 10-degree K or C temperature increase) )The enzyme's thermal inactivation rate, k_inact, also increases with temperature, leading to the bell-shaped V_M curve.  K_m, a measure of the apparent K_D of the substrate for the enzymes, increases, reflecting weaker binding.  The catalytic power, E_power = k_cat /k_inact, also decreases with increasing temperature as the slope of k_inact is generally greater than that of k_cat.  The values for the temperature axis would be different for microbes that grow best at cold temperatures (psychrophilic), moderate temperatures (mesophilic), and high temperatures (thermophilic).  

The graphs above represent temperature effects at the enzyme level. The gray rectangle represents the optimal growing conditions, which show that enzymes are poised near V_M for substrate conversion (assuming abundant substrate) but with low catalytic power. Increasing temperatures also have an effect at the microbial community level. These can affect SOC.  For example:

• After an increase in the decomposition of SOC at higher temperatures, subsequent decreases in SOC can occur due to the depletion of available substrates (as enzymes are running at V_M) and changes in carbon use among the microbial communities;
• Additional decreases in SOC due to increased oxidation and shifts in the composition of the microbial community occur;
• The levels and types of substrates for enzymes likely change;
• Increased temperatures can lead to increases in microbial community mass, which requires more substrate, but in the long-term metabolic shifts might lead to a decrease of extracellular enzymes and microbial biomass;
• Soil conditions also change with increasing temperatures, which affects biomass by changing substrate availability;
• Increased temperature lead to short-term increases in CO₂ emission due to higher microorganism metabolic rates explained by the Arrhenius equation, but additional effects caused by accompanying changes in the microbial community occur.

Complex mathematical modeling (as we saw using Vcell with metabolic and signal transduction pathways) would be needed to understand the effects of warming on SOC stores and their return to the atmosphere as CO₂. 

 

  Enzyme properties with altitude - Mount Kilimanjaro 

It is possible that the loss of SOC with climate change may be mitigated to some extent as the soil microbial community thermally adapts to a lower respiration rate/microbial biomass. As Figure 1 shows, both extracellular and intracellular enzymes must be considered.  Extracellular enzymes break down polymers like cellulose into monomers, which are transported into the cell for intracellular respiration and the formation of CO₂ by intracellular enzymes.  The extracellular (lytic) and intracellular (oxidative) enzymes might respond differently to higher temperatures.  Polymers that are hard to degrade have high activation energies, making soils with higher concentrations of these polymers more sensitive to climate warming (based on the Arrhenius equation). 

Changes in the microbial community might include shifts in the fungal/bacterial ratio, causing changes in degradation pathways and the rates of enzyme-catalyzed reactions.  At higher temperatures, such changes increase conformational flexibility, which could increase k_cat but also decrease the apparent affinity of the enzyme for the substrate, as reflected in increased K_M values. These compensatory effects might leave catalysis unaffected by increasing temperatures.

Studies have been conducted on individual degradative enzymes in soil samples from Mount Kilimanjaro.  Enzyme kinetic analyses were done at two different temperatures differing by 10⁰ C  (10⁰ C and 20⁰ C), so Q10 values could be evaluated.  The soil samples were obtained from different heights on the mountain to allow for the comparison of the kinetic parameters of enzymes from microbes adapted to different heights.   All organisms in soil from different heights would experience 10 °C, while those at the highest altitudes (3000 m) would encounter 20⁰ C only in the summer. The microbes presumably would have slightly different optimal temperatures for growth, and would likely use different adaptive mechanisms at low and high altitudes.  Keep in mind in interpreting the results below that the Q10 value determines the sensitivity of a parameter (v₀, K_M, V_M, etc.) to an increase in the temperature of 10⁰ C.

Extracellular enzyme activities in soil from one altitude

The activity of three extracellular enzymes in soil samples were studied:  β-1,4-glucosidase (degrades cellulose), N-acetylglucosaminidase (degrades chitin from fungi and peptidoglycans from bacteria), and acid phosphatase.  The first two enzymes catalyze "recalcitrant" reactions with higher activation energies.   Michaelis-Menten plots for the three enzymes in soil samples taken at one height, 2010 meters (m), are shown in Figure \(\PageIndex{3}\) below.  In addition, a plot of glucose conversion to CO₂, an intracellular process, which the authors termed "glucose" mineralization" (probably because they trapped CO₂ using OH^- to form HCO₃^-), is also shown. 

 

Figure \(\PageIndex{3}\):  Rates of reactions mediated by hydrolytic enzymes (a–c) and rates of glucose oxidation to CO₂ (d) as dependent on substrate concentration at 10 and 20 °C for the site located at 2010 m a.s.l. Symbols – experimental data, lines – approximation by Michaelis–Menten kinetics.  The red lines indicate assays performed at 20⁰ C, while the green lines are for assays run at 10⁰ C. Blagodatskaya, Е. et al. Temperature sensitivity and enzymatic mechanisms of soil organic matter decomposition along an altitudinal gradient on Mount Kilimanjaro. Sci Rep 6, 22240 (2016). https://doi.org/10.1038/srep22240.  Creative Commons Attribution 4.0 International License.  http://creativecommons.org/licenses/by/4.0/

The mineralization rate was determined using trace amounts of ¹⁴C-labeled glucose, which if fully oxidized, is converted to ¹⁴CO₂.  Given the conditions of the reactions, the added glucose did not cause microbial proliferation.  The authors used a fluorophore (4-methylumbelliferone or MUF)-labeled small substrate analogs for cellulose (MUF-β-D-glucopyranoside), chitin (MUF-N-acetyl-β-D-glucosaminide dehydrate) and for acid phosphatase (4-MUF-phosphate). Reactions were carried out in soil samples and valid initial velocities for the reaction were determined. The Km values for the glucose oxidation (mineralization) is not a valid K_M value since CO₂ would be produced from the combined actions of the enzymes in glycolysis, pyruvate dehydrogenase and the citric acid cycle.  It could be better called an "operational K_M".

For the three enzymes, the K_M at 20 °C was 25–42% larger than the V_M = k_catE_{T at} 20 °C, causing Q₁₀^KM > Q₁₀^VM.  These compensatory changes canceled any increases in enzyme activity at low substrate concentrations, but not at high ones when the enzyme was saturated.  Hence Q10 for the catabolic depolymerization reactions increased with substrate concentration.  Note, however, that the rate of intracellular glucose oxidation (mineralization) increased at all substrate concentrations going from 10 to 20 °C and the canceling effect was not detected, even at low substrate levels. The temperature response of monomer oxidation showed a strongly accelerated reaction rate instead of a canceling effect

Extracellular Enzyme activities in soils from different altitudes

Next, kinetic analyses were performed on soil samples from 2010 m (warm-adapted microorganisms) and 3020 m (cold-adapted) on the mountain. Plots of Q10 (not v₀ as in Michaelis-Menten plots) vs. substrate for these studies are presented in Figure \(\PageIndex{4}\) below to show the temperature adaption capacities of the enzymes.

Figure \(\PageIndex{4}\): The Q₁₀ values for enzymatic activities (a–c) and glucose oxidation to CO₂ (d) as dependent on substrate concentration at two altitudes. The blue and red rectangles show the concentration range at which no temperature effects occur (i.e < S_crit) with shading colors corresponding to different altitudes. The Q₁₀ values derived from experimental data are shown as symbols. The model simulations based on experimentally obtained parameters of Michaelis–Menten kinetics are shown as curves (a–c). For glucose oxidation (d) at 3020 m elevation, a non-linear trend was very weakly expressed. Bars show standard deviations of the means (n = 3).  Blagodatskaya, Е. et al. ibid.

The graphs show that Q10 for polymer degradation increased with increasing substrate concentration.  The authors defined a substrate concentration threshold (S_crit) below which K_M and V_M values canceled, so no increase in rate was seen with increasing temperature based.  The width of the rectangles is based on the best-fit dashed blue and red lines, not the data points.  The S_crit values were 35–42% larger for the 3020 m (blue rectangle) soil samples than at 2010 m (red rectangle), even though SOC was lower at that elevation.  Q10 values were always lower at S > S_crit at higher altitudes. This demonstrates that the enzymes responded less to higher temperatures at higher altitudes (blue dots and dashed lower curves), implying that the enzymes at higher latitudes demonstrated significant compensatory changes useful for microorganisms that experience a greater temperature range with larger shifts at these higher altitudes.     

Figure \(\PageIndex{5}\) below shows that the Q values generally decrease over a larger range of altitudes for both enzyme activity (panel A) and glucose oxidation (Panel B). 

Figure \(\PageIndex{5}\): The Q₁₀^total values for hydrolytic enzyme activity at saturating substrate concentrations (A) and the increase in V_max and K_m induced by a temperature increase from 10 to 20 °C for ¹⁴C-glucose oxidation (B) depending on altitude. Symbols – experimentally derived values for Q₁₀^total (B), Q₁₀^Vmax and Q₁₀^Km (A). Lines are the trend lines obtained by the best fitting of power (A) and linear functions (B) at P values < 0.05, bars show standard deviations of the means (n = 3).  Blagodatskaya, Е. et al. ibid.

Panel B shows how Q10 values for K_M apparent (green) and V_M (red) for intracellular glucose oxidation/mineralization both decreased with increasing altitude.  Again consider these K_M and V_M values to be operationally defined and apply not to an individual enzyme but in less rigorous way to all the enzymes involved in the intracellular oxidation of glucose to CO₂.  Investigators could determine these values only by fitting the kinetic data for CO₂ vs [glucose] to the Michaelis-Menten equation.  At altitudes < 2435 m, all showed Q10 K_M values > 1.9, showing that the apparent collective K_M values were very sensitive to temperature increase.  This implies the "collective" set of enzymes responsible for intracellular glucose oxidation was more conformational flexible, and higher temperatures caused significant increases in apparent K_M values.  However, at high altitudes, the Q10 values for the apparent K_M were about 1, suggesting no temperature effects on the generic structure and apparent K_M values for the enzymes.  The high-altitude enzymes were effectively temperature-stable with respect to K_M values.  V_M values were more sensitive to increasing temperatures at all altitudes, but little change was seen going from 2435 to 3020 m.  This again shows that the enzymes for microorganisms from high altitudes were more strongly adapted to temperature changes, especially at lower substrate concentrations. 

The next part can be a bit confusing.  The K_M for a given enzyme increases with increasing temperature, as shown in Figure 2.  This suggests that the apparent affinity of the given enzyme for substrates decreases, which makes intuitive sense.  Figure \(\PageIndex{6}\) shows that the Q10 for K_M (i.e. the sensitivity of K_M to a temperature increase of 10⁰ C) decreases with increasing elevation for each enzyme studied.   

Figure \(\PageIndex{6}\):  The values of Q₁₀^Km (a) and Q₁₀^Vmax (b) for hydrolytic reactions and for reactions of glucose oxidation at low and high altitudes. Bars show standard deviations of the means (n = 3).

The figure shows that both Q₁₀^Km and Q₁₀^Vmax were lower at high altitudes. Hence the enzymes in organisms from higher altitudes did not respond as strongly to temperature changes. This again suggests that larger compensatory changes are found in enzymes at high latitudes, allowing them to better adapt to the greater temperature range they would experience. 

These data suggest that thermal adaptions in the intracellular enzyme are driven more by a large range of temperatures experienced by the organisms and not the mean temperature.  Compensatory and canceling changes in K_M and V_M at low substrate concentration led to a higher S_crit in cold-adapted organisms.

Structural Mechanisms for enzyme temperature adaptation

Structure determines function.  A detailed understanding of how proteins, and more directly enzymes, adapt to temperature changes must come from detailed structural analyses that can be correlated to functions such as enzyme catalytic activity.  Two approaches have been used to study the structural bases of enzyme temperature adaptation.  One involves structural analysis of a single enzyme in organisms adapted to different temperatures.  The other involves large computational analyses of databases of protein structure. We'll discuss both.  First, let's explore orthologs (in this case, a protein from the same gene in different species) of a single enzyme, ketosteroid isomerase (KSI), from mesophilic (grown in moderate temperatures) and thermophilic (grown in warm temperatures) bacteria.

Figure \(\PageIndex{7}\) below shows structural and functional features that document KSIs temperature adaptation through changes in activity and stability.  Let's step through each of the panels in order.

Figure \(\PageIndex{7}\):  Enzyme temperature adaptation through changes in activity and stability.  Pinney et al., Science, 371. (2021). DOI: 10.1126/science.aay2784.  Reprinted with permission of the American Association for the Advancement of Science and Copyright Clearance Center.

Panel (A) shows that as the optimal growth temperature for an organism increases, the optimal temperature for selected enzyme activity also increases. Each dot represents a different species with the enzymes broadly chosen across all enzyme commission classes (i.e. the dots do not represent just KSI).  There is a strong linear correlation.    

Starting with Panel (B), we look at KSIs.  Panel B shows the mechanism of isomerization of the steroid substrate, 5(10)-estren-3,17-dione [5(10)EST] by KSI.  KSI has one of the highest k_cat values of enzymes.  The reaction changes the position of the C=C double bonds and proceeds through an enolate/oxyanion intermediate (EI) formed after the abstraction of a proton by Asp 40.  The transition state, which would have a developing negative charge on the O atom, is stabilized by proximal Tyr 16 and Asp 103 in a developing oxyanion hole. 

Panel (C) shows the KSI sequences from P. putida (a mesoKSI) and M. hassiacum (thermoKSI). The sequences are 33% identical, but some key resides (gray) are identical. Similar ones are shown in blue.  The thermophilic KSI (thermKSI) has Ser 103 instead of the often conserved Asp 103 in mesophilic organisms (mesoKSI).  D103 and S103 are shown in red.   

Now let's look at Panel (D), which shows the activity (v₀/E₀) vs substrate [5(10)EST], for the meso- and thermophilic enzymes.  At a nominal temperature (25⁰ C, top left panel), the thermoKSI shows little activity.  At their optimal growth temperatures (30⁰ C for the mesoKSI and 65⁰ C for thermoKSI, bottom left), the thermoKSI has both a higher V_M=k_catE₀, and K_M at 65⁰ C.  The higher K_M is consistent with the idea that K_m values are usually higher at higher temperatures. The derived k_cat and k_cat/K_M values are shown in the adjacent histogram.  Remember that k_cat is a measure of how many bound substrate molecules are converted to product per sec (at saturating substrate concentrations).  The parameter k_cat/K_M is a measure of the effective biomolecular rate constant for product formation at low substrate concentrations ([S] <<K_M). 

From an evolutionary perspective, early ancestral enzymes probably arose in warmer environments.  When the earth cooled, enzymes had to "solve" the problem easily apparent from the Arrhenius equation (the rate of reactions decreases with decreasing temperatures).  Hence evolution would lead to structural changes that would facilitate either higher k_cat values, lower K_M values, or both, at lower temperatures. We've seen in the examples above that K_M decreases with decreasing temperatures, so evolutionary pressures would more likely lead to increased k_cat values. This is consistent with localized changes in protein dynamics as modulators of k_cat. The evolutionary pressure to maintain stability would be low since proteins become more stable at lower temperatures.

Now the question arises, how thermally stable are the meso- and thermKSI?  Urea denaturation experiments were used to determine the ΔG^0 H2O_U for unfolding of the enzyme, as described in Chapter 4.12.  Panel (E) shows urea denaturation curves for mesoKSI (black) and thermoKSI (red) monitored by changes in internal tryptophan fluorescence (top) and stabilities extrapolated to 0 M urea (ΔG^H2O_U) (bottom). The denaturation curve for thermoKSI is significantly shifted to the right.   The calculated values for ΔG^0 H2O unfolding are +18.5 kcal/mol (mesoKSI )and about +25.3 (thermoKSI), a +6.8 kcal/mol difference.  These values would be - 18.5 kcal/mol (mesoKSI) and about -25.3 (thermoKSI) for the reverse folding reaction (unfolded ↔ folded transition).  

Figure \(\PageIndex{8}\) shows an interactive iCn3D models  of the bacterial ketosteroid isomerase from the mesophilic bacteria Pseudomonas Putida (left) and from the thermophilic bacteria Mycobacterium hassiacum (right).

Figure \(\PageIndex{8a}\):  Mesophilic Ketosteroid Isomerase D40N mutant (monomer) from Pseudomonas Putida (pKSI) bound to 3,4-dinitrophenol (6C17).  (Copyright; author via source).  Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...kH877KZKPxWsGA	Figure \(\PageIndex{8b}\): Thermophilic Ketosteroid Isomerase D38N mutant (monomer) from Mycobacterium hassiacum (mhKSI) bound to 3,4-dinitrophenol (6P44).  (Copyright; author via source).  Click the image for a popup or use this external link:  https://structure.ncbi.nlm.nih.gov/i...YbGw5zr2dRpnK8

Both structures have a bound 3,4-dinitrophenolate, a stable oxyanion and transition state analog. The corresponding active site side chains are shown in color sticks.  Just one monomer of the dimer for each protein is shown for clarity.  The key active-site residues F86, V88, V101, and D103 in mesoKSI are replaced by W86, L88, I101, and S103 in thermoKSI (all very conservative except for D103S).  A water molecule forms a bridging hydrogen bond from S103 to the oxyanion in the phenolate.

 

Figure \(\PageIndex{9}\) below shows the key change in Asp 103 (see the mechanism in Fig. 7B) in mesoKSI to Ser 103 + H₂O in thermoKSI

Figure \(\PageIndex{9}\): Change from Asp 103 in mesoKSI to Ser 103 + H₂O in thermoKSI

 

Asp 103 is initially protonated with a pKa is >9, much higher than in an aqueous solution (3.7).  The hydrogen bond from the mesoKSI D103 to the phenolate is stronger than the bridging one from Ser 103 in the thermoKSI.  This arises from the increased polarity of the OH on a carboxylic acid (Asp) compared to an alcohol (Ser). In addition, the hydrogen bond distance from the bound water to the phenolate is longer than from Asp 103. Hence the Asp 103 in the thermoKSI improves enzymatic stability.  In contrast, at lower temperatures, thermoKSI is less active, but at higher temperature it is more stable. The role of Ser 103 in stabilizing the folded state is shown in Figure \(\PageIndex{10}\) below

Figure \(\PageIndex{10}\): Roles of Asp 103 and Ser 103 in the folding to unfolding transition of KSI

When mesoKSI unfolds, Asp 103, which is protonated and not accessible to solvent in the native state, becomes solvent exposed on denaturation.  Its pka drops, which leads to its deprotonation.  This extra deprotonation step stabilizes the unfolded state (pulling the reaction to the right), making thermoKSI less thermally stable.  In contrast, Ser 103, on solvent exposure, does not deprotonate, so the unfolded state is not additionally stabilized.   Hence Ser 103 leads to greater stability of the folded thermoKSI.  The D103/S103 change is found in many KSI from many bacteria.

Here are some additional findings:

• The structures of mesoKSI and thermoKSI are highly similar even though they have only 33% sequence identity.  Figure \(\PageIndex{11}\) shows the conformational changes in the monomeric ketosteroid isomerase (KSI) going from the mesophilic enzyme (6C17, cyan) to the thermophilic one (6P44, magenta) enzymes

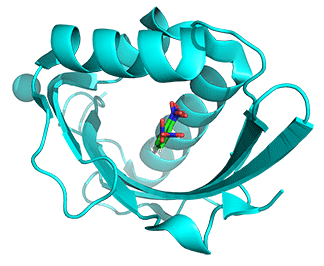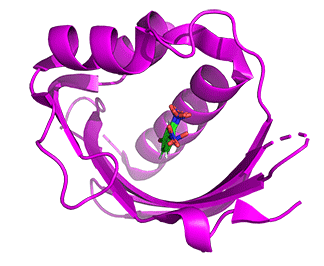
Figure \(\PageIndex{11}\):  Conformational changes in the monomeric KSI going from the mesophilic enzyme (6C17, cyan) to the thermophilic one (6P44, magenta) enzyme

• The F86W change in the thermoKSI stabilizes the conformation of S103 to maximize its stabilization of the oxyanion in the oxyanion hole and allows high-temperature activity.
• Other KSI orthologs and mutants show higher enzyme activity if they have D103. 
• Changing key residues at 86, 88, and 101 in mesoKSI to those found in the thermoKSI additionally increased the stability of the mesoKSI
• Analysis of 1140 KSIs showed that the fraction containing D103 decreases with increasing growth temperature, and the fraction containing S103 increases.  

It appears that the thermal adaption of KSI occurs mostly through one amino acid change (D103S). The change reduces k_cat for the mesoKSI 10x at low temperatures but greatly increases stability at high temperatures.

This switch and compensatory changes in activity and stability suggest that protonated Glu and Asp side chains involved in activity might be changed to other amino acids that confer more stability but reduce activity.  A conserved and protonated active site Glu is found in glycosidases from high-temperature orthologs.  Likewise, a protonated Asp side chain is found in thioredoxin. As a control, a change from a protonated Glu in triosphosphate isomerase distal to the active site to a Gln shows no effect on catalysis and was not found in thermophiles.   It should be noted that not all stabilizing mutations decrease activity since many examples are known that don't. 67 protonated Asp and Glu side chains were identified in the PDB, 14 of which were replaced in high-temperature orthologs.

Conservation of chaining pairs of amino acids between mesophilic and thermophilic organisms.

Are there other broadly found changes in amino acids (in addition to Asp/Glu) at each position in a mesophilic protein and its thermophilic ortholog?  Computational analysis in 2194 enzyme families in 5582 bacterial species (for a total of 17 million amino acid pairs) were performed to explore this question.  Half of all families had an amino acid at a given position which correlated with growth temperature, resulting in almost 160,000 key positions. The results of this study are broadly outlined in Figure \(\PageIndex{12}\) below.  

Figure \(\PageIndex{12}\): Examination of temperature-associated residues and their interactions. Pinney et al., ibid. Reprinted with permission of the American Association for the Advancement of Science and Copyright Clearance Center.

Let's explain each part of this complex figure.

Panel (A) - Preferences in the types of amino acids associated with high or low-temperature growth: Panel (A) shows the difference in frequency of association of given amino acids with high to low temperatures.  Some amino acids were associated with low-temperature growth. These include alanine (A), glutamine (Q), and aspartate (D), as in KSI).  Others were associated with high-temperature growth (E, I, Y and K).  F

Panel (B)  - Identities and frequencies of site-specific residue changes across temperature growth conditions:  Now let's see how a specific acid changes in going from mesophilic (low T) to thermophilic (high T), which show key temperature-dependent amino acid changes. Panel (B) shows the frequency of observed site-specific changes in temperature-associated residues. The “+” indicates that the frequency of a change (such as Leu to Ile) is significant in comparison to the opposite change (Ile to Leu). Indeed the darkest square is from a Leu (at low temperatures) to Ile (at high temperatures change.  Other darker squares show these changes occur going from low to high temperature-adapted bacteria:  V → I, R → L, and D → E.  The specific one found for KSI, D → S, does not stand out, most likely because of the diverse types of enzymes included in the analysis. 

Panel (C) - Identities and frequencies of physically interacting temperature-associated residue pairs (in a single protein):   If one amino acid changes in going from a low to a high-temperature ortholog, it is likely that the original and changed amino acids physically contact different nearby amino acids in their respective protein.  Panel (C) shows the difference in frequency of association with high vs. low-temperature growth bacterial enzymes for "all possible physically interacting pairs of residues (made up of residues R₁ and R₂) that change concomitantly with the growth temperature".   The darker blue squares show interacting residue pairs found more often in low-growth temperature enzymes, while darker maroon squares show contacting pairs in high-growth temperature proteins.  The asterisk shows pairs are statistically significant.

One of the darkest maroon squares (high-temperature enzymes) shows an Ile-Ile interaction pair.   The vertical column above Ile (high growth) in Panel B shows that changes to Ile in high-temperature enzymes occur frequently from 6 different amino acids found in low-temperature enzymes. Ile might be favored over Val to maximize buried hydrophobic surface area.  Also, compared to Leu, it has great conformation flexibility and could better pack empty spaces in protein interiors.  

A Lys to Glu (K to E) interaction is strongly associated with high-temperature enzymes, while an Arg to Asp (R to D) interaction is strongly associated with the low-temperature enzyme.  This implies that simply increasing the number of salt bridges (ion-ion interactions) does not make a protein more thermally adaptable.   Lys salt bridges would have greater conformational flexibility than those using Arg.  The same applies to Glu compared to Asp.  Lys also has the largest hydrophobic surface area, which could enhance hydrophobic packing.  Since Arg has hydrogen bond donors requiring more adjacent hydrogen bond acceptors, Arg use might depend more on adjacent amino acids and not just a binary pair.  

In summary, these results are more nuanced than previous explanations for high-temperature stability:

• increasing branched chain residues like Ile, Leu, and Val in the packed hydrophobic core.  Indeed, as seen in Panel B,  the most frequent amino acid change observed are from Leu/Val in low-temperature growth orthologs to Ile in high-temperature growth ones.  These are all branched-chain amino acids. They occur 2-3x more frequently than the reverse, Ile in low-temperature growth to Leu/Val in high-temperature growth enzymes.  In fact, Panel C shows that Ile preferentially interacts with another Ile in high temperature adapted enzyme.  Hence stability is not just improved by substitution with any hydrophobic side chain.
• increasing number of salt bridges  (ion-ion interactions) and hydrogen-bonding interaction charged side chains. There are more charge side chains and salt bridged in thermophilic proteins. However, the above data shows a clear preference for Lys in thermophilic proteins as changes from Arg to Lys are common in that group as shown in Panel B.  Likewise, Asp to Glu changes from low to high temperature-adapted proteins are 3 times more probably than the reverse.  In addition, Panel C shows that interactions between Lys and Glu are most strongly associated with high temperature-adapted proteins, while Arg and asp interactions are most often in low temperature-adapted proteins.

Allosterism and Thermal Changes

As we mentioned before, increasing temperature can cause local effects in a protein, instead of large global changes that obviously lead to denaturation at high temperatures. Changes occurring in the active site can clearly affect k_cat, K_M, and k_cat/K_M.  Allosteric effects also occur.  The protein imidazole glycerol phosphate synthase (HisFH) is a heterodimer with two active sites, so it is considered a bienzyme.  The H subunit is a glutaminase, which cleaves glutamine into glutamine acids and ammonia, which can diffuse through a channel to the active site of the F subunit, the cyclase.  The active form of the enzyme occurs only when both substrates are bound resulting on long-range allosteric activations. In particular, the oxyanion hole in the H subunit is formed in the activated form which allows the stabilization of the tetrahedral transition intermediate in the hydrolysis of glutamine.  

Figure \(\PageIndex{13}\) shows an interactive iCn3D models  of the heterodimeric imidazole glycerol phosphate synthase complex (7AC8)

Figure \(\PageIndex{13}\):  (Copyright; author via source). Heterodimeric imidazole glycerol phosphate synthase complex (7AC8). Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...S5MbiiA9bDvDQ8.

The HisH (glutaminase) subunit is shown in orange with a molecular surface and the bound substrate (spacefill), glutamine.  The HisF subunit is shown in cyan with a bound substrate.

An allosteric effector molecule can bind in the active site of His F and induce long-range conformational changes in this HisH active site which increases its activity 5000x.  The structures involved are shown in Figure \(\PageIndex{14}\) below.

Figure \(\PageIndex{14}\):  Imidazole glycerol phosphate synthase (IGPS) from the thermophile Thermotoga maritima (T. maritime).  Maschietto, F., Morzan, U.N., Tofoleanu, F. et al. Turning up the heat mimics allosteric signaling in imidazole-glycerol phosphate synthase. Nat Commun 14, 2239 (2023). https://doi.org/10.1038/s41467-023-37956-1.  Creative Commons Attribution 4.0 International License.  http://creativecommons.org/licenses/by/4.0/.

IThe HisF and HisH subunits are colored respectively in green-to-blue and red-to-yellow gradients, respectively, and separated by a dotted line which marks the interface between HisF and HisH. The labels (fα2, fα3, fβ2, loop1, hα1, Ω-loop) indicate secondary structure elements that are directly involved in the allosteric regulation.  

Molecular dynamics and NMR studies have shown that increases in the temperature lead to conformational changes resembling those that occur on binding of the allosteric effector at room temperature.  As the temperature of the apoenzyme (no substrates or effects bound) increases from 30 °C to 50 °C, the dynamics and structure increasingly resemble the state induced by the effector.  Increasing temperatures from climate change are likely to cause subtle conformational and dynamic changes in all proteins with some having negative consequences.

Thermal determinants of yeast metabolism

With this basic background, we can attempt to understand the thermal determinants for entire metabolic pathways. This has been attempted in the yeast Saccharomyces cerevisiae, a eukaryotic organism with optimal growth around ~30 °C, extremely limited growth at 40 °C, and no growth/death at 42 °C.

Mathematical modeling all metabolic pathways in a cell is a daunting task. Accurate concentrations, rate constants, and dissociation constants are needed for all reactions.  Genome-scale metabolic models (GEM) use a multitude of constants that are experimentally or computationally determined.  There are usually significant uncertainties in the parameters used in the model.  Bayesian statistics has been used to decrease these uncertainties. In Bayesian statistics, parameters and models are updated with the known values and information.  It is similar to machine learning models, which uses data to train the model and refine it.

A Bayesian model for S. cerevisiae was used as it is the most abundantly used organism in industry and has many GEMs.  The GEM used was the enzyme-constrained GEM (ecGEM).  It was then further developed into the enzyme and temperature-constrained GEM (etcGEM), which, in addition, incorporates the temperature dependence of both the concentration of the native enzyme (E_N) and kcat for the enzyme. For each enzyme, the melting point (T_M), the change in heat capacity (ΔCp) for the transition state, and the optimal temperature (T_opt) were included.  We discussed both (T_M) and the change in heat capacity (ΔCp) for proteins in Chapter 4.9.  In addition, another term for non-growth associated maintenance (NGAM) of the cells, which is also temperature-dependent, was included.  Examples of non-growth associated maintenance include maintaining membrane potential, turgor pressure, normal protein refolding and DNA repair.

The Bayesian models reproduced the datasets well. Using the models, key enzymes that control the flux through metabolic pathways were determined at each temperature.  The most rate-limiting enzyme at superoptimal temperature in yeast was squalene epoxidase (ERG1), found in sterol metabolism pathways.   Replacing the S. cerevisiae enzyme with one from a thermotolerant yeast strain led to better growth than the wild-type cells. 

Figure \(\PageIndex{15}\) below the complexity and extent of the metabolic proteins and pathways of the enzyme-constrained GEM (ecGEM).

Figure \(\PageIndex{15}\:  Metabolic proteins and pathways included in the enzyme-constrained GEM. Benjamín J Sánchez et al., Molecular Systems Biology (2017)13:935.  https://doi.org/10.15252/msb.20167411.  Creative Commons CC BY

 

(add soon:  ecYeast7 model (both constrained and unconstrained; each as.mat,.sbml and.txt files): GitHub  (https://github.com/SysBioChalmers/GECKO/tree/v1.0/Models)

Now, let's explore some of the results of the study.  Figure \(\PageIndex{16}\) below shows how the temperature dependencies of proteins were incorporated into the enzyme-constrained GEMs.

Figure \(\PageIndex{16}\): Using Bayesian statistical learning to integrate temperature dependence in enzyme-constrained GEMs.  Li, G et al., Nat Commun 12, 190 (2021). https://doi.org/10.1038/s41467-020-20338-2.  Creative Commons Attribution 4.0 International License.  http://creativecommons.org/licenses/by/4.0/.

Panel a shows the complexity of the metabolic network used to produce the ecYeast7.6, shown in greater detail in Fig. 13 above, and how E_N and k_cat depend on temperature.  

Panel b shows how a two-state denaturation model was used.  [E]_N is the enzyme concentration in the native state; T_opt is the optimal temperature at which the specific activity is maximized; T_m and T₉₀ are temperatures at which there is a 50 and 90% probability that an enzyme is in the denatured state, respectively.  In Chapter 4.4 we indicated that for a reversible two-state transition, T_M is the temperature at which half of the enzyme is native, and half denatured, giving a K_eq for the N ↔ D equilibrium of 1.

Panel c shows how k_cat depends on temperature.  The insert show how the heat capacity change from E+S to the E-transition state.  We have previously seen that the ΔC_P > 0 for protein unfolding, and this +ΔC_P value is a signature of the hydrophobic and occurs when nonpolar groups become more solvent exposed.  We have shown previously that enzymes bind the transition state more tightly than the substrate.  This -ΔC_P is more in line with the latter.   

Panel d shows the temperature dependence of enzyme's specific activity, r, as a function of temperature, which is determined by E_N (panel B) and k_cat (panel C).

Now we can explore the outputs of the ecGEM run with the separate added effects of temperature on NGAM, k_cat, and E_N (denaturation). Finally, the combined etcGEM was run.  The combined etcGEM was able to produce the observed outcomes in yeast growth.  Given that the contributions of each of the three factors, NGAM, k_cat, and protein denaturation, to whole-cell growth could be modeled. The outcomes from these models as a function of temperature are shown in Figure \(\PageIndex{17}\).  They support the notion that the growth rate of yeast is explained by temperature effects on its enzymes.  

Figure \(\PageIndex{17}\): Fig. 3: Yeast growth rate is explained by temperature effects on its enzymes.  Li, G et al., ibid

This figure shows how the temperature dependence of different processes combines to affect the growth rate. EC is the prediction from the enzyme contained GEM, —predictions with the enzyme-constrained model;  ec+NGAM includes temperature effects on nongrowth associated maintenance; ec+k_cat(T) incorporates the temperature effects on enzyme k_cat values; ec+denaturation(T) incorporates the temperature effects on enzyme denaturation.  Finally, in the etc model, the enzyme and temperature-constrained model incorporates temperature effects on all three (NGAM, k_cat and enzyme denaturation) into ec model. The solid lines indicate median values and shaded areas indicate regions between the 5th and 95th percentiles (n = 100). 

Here are some summarized results:

• <29 °C, only temperature-dependent k_cat affected the cell growth rate (green line under the orange etc line <29 °C;
• at 29 °C <T < 35 °C, both k_cat and NGAM (gray line) determined the growth rate;
• at T > 35 °C, enzyme denaturation at major effects and by 40 °C was dominant,

Figure \(\PageIndex{18d-e}\) shows using images how the temperature dependencies of the factors E_N, k_cat and r (specific activity) on yeast growth.  A phenomenal amount of data is displayed in these images.

Figure \(\PageIndex{18d-e}\): Fig. 3: Yeast growth rate is explained by temperature effects on its enzymes.  Li, G et al., ibid

Panel d shows the probability that a given enzyme is in the native state.  Think of the y-axis as increasing 1 pixel at a time from bottom to top, with each new added pixel representing a different enzyme for a total of 764 enzymes along the y-axis.  The x-axis shows with each pixel at a given y-axis  if the enzyme is native that temperature

The interface between bright (native) and black (denatured) on the right side of the image shows that some enzymes (top) become unfolded at 40⁰C, while some don't unfold until close to 60⁰C

Panel e shows normalized k_cat values of 764 enzymes at different temperatures. The brightest white pixels show the highest k_cat values. The image clearly shows the brightest vertical band at around 30⁰C, the optimal growth temperature of yeast.   

Panel f  shows the normalized specific activities (r) of 764 enzymes at different temperatures. Again the highest specific activity is centered around  30⁰C.

Note in Fig. 15d that most enzymes also denature at temperatures < -10 ⁰C, but cells were not viable under those conditions.

The etcGEM was able to replicate a finding that above 37 °C, yeast cells switch from respiration to partial fermentation accompanied by a larger flux through glycolysis.  This occurred because of a decrease in specific activities of enzymes with increasing temperature, which constrains metabolism.  In addition, the total protein concentration reaches a limit and can't increase further, which could have increased enzyme activity.  Along with an increase in glycolysis, mitochondrial ATP production decreases.  Respiration produces more ATP per mole of glucose, but glycolysis/fermentation produces more ATP/protein mass so when protein concentration reaches a maximum, glycolysis is more efficient.

Lastly, the etcGEM was used to find the enzymes whose flux changed most at superoptimal temperatures. (We introduced the flux control coefficient in Chapter 14.3). The results of this modeling are shown in Figure \(\PageIndex{19}\) below.

 

Figure \(\PageIndex{19}\): Flux control coefficients at superoptimal model for yeast. 

One enzyme stands out in Panel a, ERG1, squalene epoxidase, an enzyme involved in sterol oxidation. If the wildt-type enzyme was replaced with a temperature-insensitive ERG1, the specific growth rate increased significantly (over 55%). 

 

What does this have to do with climate change? Life's Thermal Tolerance and Limits

We've just explored the molecular and metabolic adaptations that allow organisms to thrive at higher temperatures. The question is how quickly present life can adapt to global warming caused by increasing greenhouse gases.  Life on the planet will adapt, but the diversity of life forms in the biosphere will change. Five mass extinction have occurred over the last 450 million years up until the present, as shown in Figure \(\PageIndex{20}\) below.

 

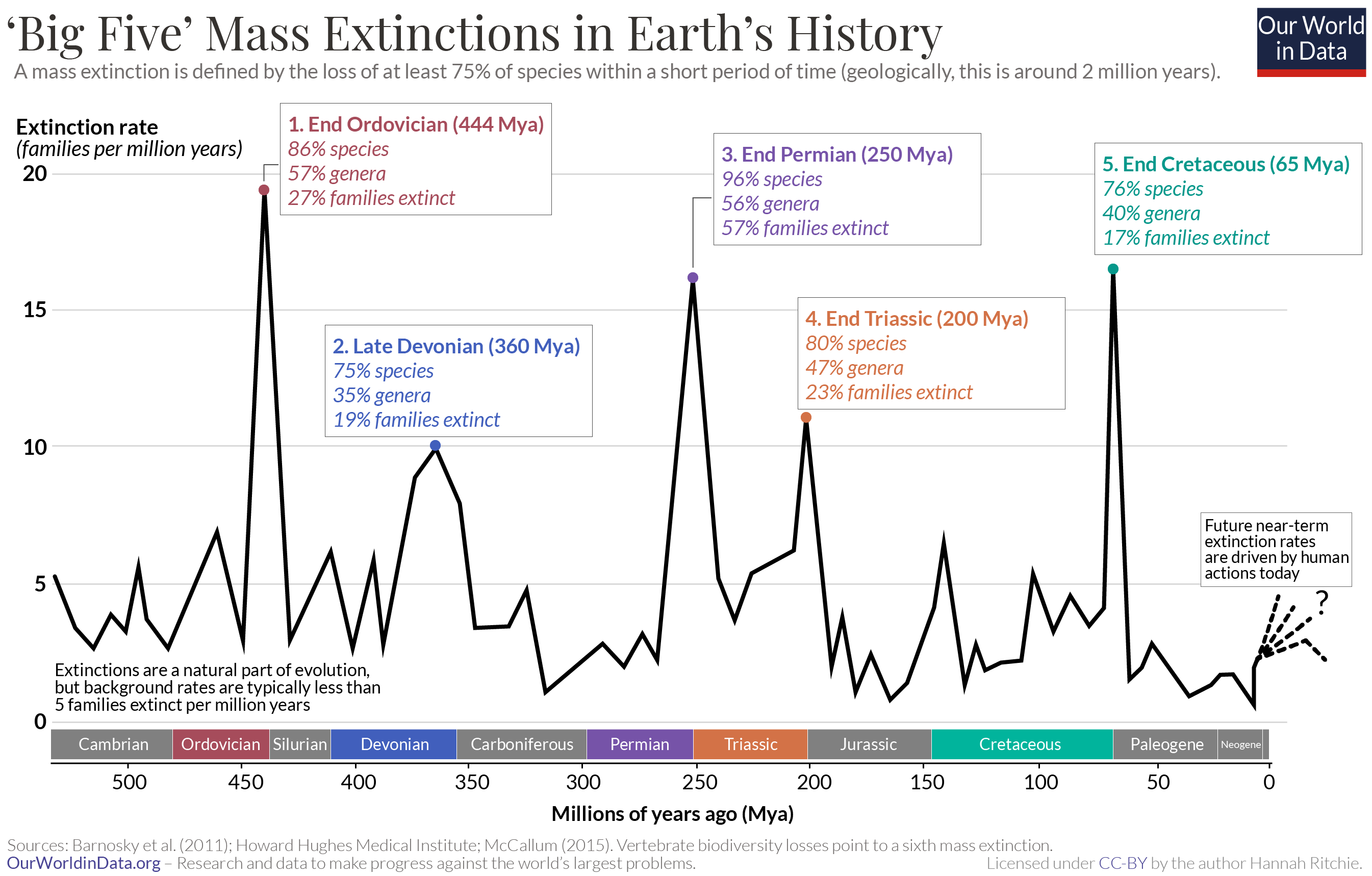
Figure \(\PageIndex{20}\): Five mass extinction over the last 450 million years. Hannah Ritchie. Our World in Data.  https://ourworldindata.org/mass-extinctions.  Creative Commons BY license. 

Many factors, often interrelated, can contribute to mass extinction.  These include volcanism, asteroid impact, climate change, ocean anoxia, and the release of methane from ocean hydrates and permafrost. All are correlated with increased temperatures. as shown in Figure \(\PageIndex{21}\) below.  It documents the correlation between temperature changes and the extinction rate for marine animals over the last 450 years. The gray bars highlight the extinction cycle.

Figure \(\PageIndex{21}\): Temperature change and extinction rate over the past 450 million years.  Song, H., Kemp, D.B., Tian, L. et al. Nat Commun 12, 4694 (2021). https://doi.org/10.1038/s41467-021-25019-2.  Creative Commons Attribution 4.0 International License.  http://creativecommons.org/licenses/by/4.0/.

Pane a shows the largest magnitude of temperature change (ΔT, absolute value) in each time interval (bin) 

Panel b shows the highest rate (R, absolute value) of temperature change in each time bin, defined at the million-year (Myr) scale. 

Panel c shows the generic extinction rates of marine animals calculated using gap-filler methods using data from the Paleobiology Database. The Big Five extinctions occurred in the end-Ordovician (OS), Frasnian-Famennian transition (FF), Permian-Triassic transition (PT), Triassic-Jurassic transition (TJ), and Cretaceous-Paleogene transition (KPg). Vertical bars show mean ± 1 x standard deviation (see Methods). O Ordovician, S Silurian, D Devonian, C Carboniferous, P Permian, T Triassic, J Jurassic, K Cretaceous, Pg Paleogene, N Neogene. Dark cyan, blue, and red dots represent ΔT, R, and extinction rate, respectively. 

The authors suggest that a temperature change of >5.2 °C and a rate of >10 °C/Myr would lead to a new extinction rate comparable to the "Big Five".  A rise of 5.2 °C is in the upper range (but likely only with human inaction to prevent it) of IPCC projection. The present rate of temperature increase (almost 2 °C/200 years) is unprecedented in at least the last 3 million years.  So it appears that we are headed to a 6^th mass extinction, caused by a combination of environmental degradation, pollution and climate change created by humans.

Rothamn has suggested that we can tip over into an "official" mass extinction depending on the magnitude and the rate of change in the carbon cycle.  If long-scale changes occur too quickly and organisms can't adapt, extinction follows.  If the changes occur on a short time scale (as it happening now), the size of the change is a key factor.   His analysis suggests that a key factor is anthroprogenic-related increases in ocean CO₂.  A threshold of 310 Pg (Gt), which we could reach by 2100, could officially trigger the sixth mass extinction.  However, many would argue that we are already in the 6th extinction cycle. For example, of about 30,000 terrestrial vertebrate species, about 1.7% (515 species) are on the verge of extinction (having <1000 individuals).   77 mammal and bird species have lost most of their populations.

When it comes to how organisms will adapt to our present climate change, Hochahka and Somero ask 6 relevant questions:

1. What is the thermal optima and how much change leads to suboptimal or lethal conditions?
2. What mechanisms set upper limits?
3. How close do organisms live to the limits of their thermal tolerance?
4. To what extent can organisms acclimatize to temperature increase?
5. When are genetic changes necessary for survival?
6. Does the acquisition of heat tolerance reduce cold tolerance? 

More simply, we can ask if organisms can survive and thrive and at what cost.  Humans most assuredly can survive a warming world, but if temperatures become too high, they will not thrive and parts of the world we become inhabitable to them without great economic, social, political, and cultural costs.  Some organisms will become extinct.  Mass migrations of all species will occur as they seek more habitable environments.

In an evolutionary sense, species occupy environments in which they can survive and adapt.  Our climate has been fairly constant since the end of the last ice age, about 12,000 years ago.  Climatic changes that make an environment suboptimal depend on how sensitive an organism is and how close it lives to its thermal limits.  We have already documented the thermal limits of individual enzymes as well as whole metabolic systems 

As you learned in introductory chemistry, multiple linked reactions can only go as fast as their slowest step.  An analogous insight is that a chain is only as strong as its weakest link.  It may be the membranes, not proteins, are the weakest link with respect to temperature adaptation as higher temperatures alter phases and subphases like rafts with lipid bilayers which in turn can disrupt the activity of membrane proteins.  Membrane functions (permeability, endo- and exocytosis, and maintenance of transmembrane potentials) are also very important. 

Temperature effects on neural communication in synapses might be key. An interesting example is a particular Antarctic fish, which after long exposures to 4 ⁰C, dies if temperatures are raised to around 9⁰C.  Synaptic transmission through the acetylcholine receptor is altered as the amount of acetylcholine in the synapse increases and the rate at which it is degraded by acetylcholinesterase decreases.   

The lethal temperature for an organism can depend on many factors, including the rate of temperature increase, the length of exposure,  previous long-term acclimatization, and for humans, humidity. Humans can't dissipate body heat without sweating if the external temperature is >37⁰C (average body temperature).  If the humidity is high enough, sweating is ineffective in dissipating heat.  Since metabolism produces heat, the body temperature can increase past 37⁰C even if the external temperature is lower.  A lethal limit for humans can occur as low as 29⁰C (84⁰C) at a relative humidity of 85%. Even now, about 30% of the human population is exposed to lethal thresholds at least 20 days/yr, and this will only grow as temperatures and humidity increase.

Comparisons of similar species (congeneric) that live in intertidal regions (region above the water level at low tide and underwater at high tide) vs. subtidal regions (close to a shore but always submerged) show significant differences.  Organisms living in intertidal regions will experience a higher range of temperatures.  19 species of congeneric porcelain crabs exist that inhabit different latitudes and vertical depths in intertidal and subtidal regions. Intertidal crabs that experience a highly variable temperature region are exposed to temperatures much closer to their lethal temperature limit, showing the T_lethal - T_{max habitat} get smaller. Heart function and neural activity at higher temperatures appear to be weak links in survival.  Heat shock protein function is also different in congeners of marine snails.  Lethal temperatures appear to be those at which protein synthesis dramatically decreases. Repair to damaged protein is decreased, which limits vertical migration to lower temperatures and can make organisms more susceptible to predation.  These effects can occur over a small increase in temperature (a few degrees Celsius).  It becomes more important to heed the warnings by the IPCC to limit global average temperature increases to 1.5 to the more likely 2.5⁰C range.

Laboratory experiments in directed evolution show that an organism's thermal tolerance can be increased, but there are limits. E. Coli can live at a variety of temperatures and experiments to evolve them at 37 ⁰C (human gut temperature), at 42 ⁰C (close to their lethal limit), and in an environment with fluctuating temperatures (between 32 ⁰C - 42 ⁰C) have been conducted. Over 1000s of generation, the rate of evolution was highest in the 42 ⁰C group.  The group that evolved at fluctuating temperatures was better adapted to both higher and lower temperatures.  Under no circumstance did E. Coli evolve into a thermophilic species, which would require novel gene function and not just a small set of mutations that allow for more optimal values of k_cat and K_M for enzyme catalysis.