5.2: Techniques to Measure Binding

Search Fundamentals of Biochemistry

Learning Goals 

(Learning goals written by Claude, Sonnet 4.6, Anthropic)

Experimental Methods for Determining K_D

• Compare the principles, requirements, and limitations of six experimental approaches for measuring K_D — gel filtration chromatography, membrane filtration, equilibrium dialysis, precipitation, spectroscopy, isothermal titration calorimetry (ITC), and surface plasmon resonance (SPR) — distinguishing methods that require physical separation of free from bound ligand from those that do not, and explaining the experimental conditions under which each is most appropriate.
• Explain why ITC binding curves of ΔH per injection vs. molar ratio (L₀/M₀) are sigmoidal rather than hyperbolic — connecting this to the condition where L₀ is not >> M₀ and the differential nature of the measurement (heat per injection equals the change in ML between successive injections) — and describe how a single ITC experiment simultaneously yields K_D, binding stoichiometry (n), ΔH°, and, by calculation, ΔG° and ΔS°.
• Describe the physical principle underlying surface plasmon resonance (SPR) — how ligand binding changes the refractive index at the gold sensor surface, shifting the resonant angle of totally internally reflected light — and explain how the time-resolved SPR signal (sensorgram) provides both kinetic rate constants (k_on and k_off) and equilibrium K_D values.

Molecular Determinants of Binding Affinity and Extreme Binding

• Interpret antibody-antigen binding data (H-bonds, van der Waals contacts, salt bridges, buried polar and apolar surface areas) to conclude that increased binding affinity correlates primarily with increased buried apolar (hydrophobic) surface area rather than with increased numbers of hydrogen bonds or salt bridges, and connect this finding to the thermodynamic contribution of the hydrophobic effect to protein-ligand stability.
• Explain how the extraordinarily tight binding of Cu¹⁺ to CueR (K_D ~ 10⁻²¹ M) is determined using CN⁻-buffered free metal ion concentrations derived from linked equilibria — and discuss the biological implication that essentially no free Cu¹⁺ exists in the E. coli cell, yet a single ion is sufficient to activate CueR-dependent gene expression controlling copper homeostasis.
• Explain how cells achieve metal ion selectivity and delivery using the Irving-Williams stability series, metal chaperones, metal transporters, metal sensor proteins, restricted access to binding sites, and metal-induced conformational changes — and connect the concept of competitive metal binding to the regulation of metalloprotein assembly.

The Cellular Binding Environment

• Explain how molecular crowding in cells (total macromolecule concentrations up to 400 mg/mL, with 5–40% of cellular volume occupied by large molecules) differs fundamentally from dilute in vitro binding assays — predicting how macromolecular crowding affects effective concentrations, diffusion rates, and binding equilibria — and critically evaluate the extent to which in vitro KD measurements reflect the true binding behavior of proteins inside living cells.

It is often essential to determine the K_D for a macromolecule:ligand (ML) complex. With that number and the concentrations of M and L in the system, we can then predict if M is bound under physiological conditions. Again, this is important since whether M is bound or free will govern its activity. To determine K_D, you need to determine ML and L at equilibrium. How can we differentiate free from bound ligands? The following techniques allow such a differentiation.

Techniques that require the separation of the bound from the free ligand.

It is important that these techniques do not perturb the equilibrium of M + L ↔ ML during separation.

Gel filtration chromatography

Add M to a given concentration of L. Then elute the mixture on a gel filtration column using the free ligand at the same concentration. The ML complex will elute first and can be quantified. If you measure the free ligand coming off the column, it will be constant after the ML elutes, except for a single dip near where the free L would elute if the column were eluted without free L in the buffer solution. This dip represents the amount of ligand bound by M.

Membrane filtration

Add M to radiolabelled L, equilibrate, and then filter through a filter that binds M and ML. For instance, a nitrocellulose membrane binds proteins irreversibly. Determine the amount of radiolabeled L on the membrane, which equals [ML].

Precipitation

Add a precipitating agent, such as ammonium sulfate, which precipitates proteins (both M and ML). Determine the amount of ML.

Techniques that do not require the separation of bound from free ligand.

Equilibrium dialysis

Place M in a dialysis bag and dialyze against a ligand solution whose concentration can be determined using radioisotopic or spectroscopic techniques. At equilibrium, determine the free L by sampling the solution surrounding the bag. Using mass balance, the amount of bound ligand can be determined, which gives ML for a 1:1 stoichiometry. Repeat at many different ligand concentrations.

Spectroscopy

Find a ligand whose absorbance or fluorescence spectra change when bound to M. Alternatively, monitor a group on M whose absorbance or fluorescence spectra change when bound to L.

Isothermal titration calorimetry (ITC)

In ITC, a high-concentration solution of an analyte (ligand) is injected into a cell containing a solution of a binding partner (typically a macromolecule like a protein, nucleic acid, or vesicle). Figure \(\PageIndex{1}\) shows an isothermal titration calorimeter cell,

Figure \(\PageIndex{1}\): Isothermal Titration Calorimeter Cell

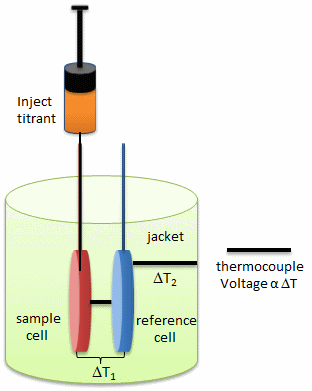
On binding, heat is either released (an exothermic reaction) or absorbed, resulting in a small temperature change in the sample cell compared to the reference cells containing only a buffer solution. Sensitive thermocouples measure the temperature difference (ΔT₁) between the sample and reference cells and apply a current to maintain the difference at a constant value. Multiple injections are made until the macromolecules are saturated with the ligand. The enthalpy change is directly proportional to the amount of ligand bound at each injection, so the observed signal attenuates with time.

The observed enthalpy change must be corrected for the enthalpy change on simple dilution of the ligand into buffer alone, which will be determined in a separate experiment. The enthalpy changes observed after the macromolecule is saturated with the ligand should be the same as the enthalpy of dilution of the ligand. A binding curve showing enthalpy change as a function of the molar ratio of ligand to binding partner (L₀/M₀), not free L or Lo, is generated and mathematically analyzed to determine K_D and the binding stoichiometry. Figure \(\PageIndex{2}\) shows a typical isothermal titration calorimetry data and analysis

Figure \(\PageIndex{2}\): Typical isothermal titration calorimetry data and analysis. http://www.microcalorimetry.com/index.php?id=312

The example above clearly shows that the binding reaction is exothermic. But why is the graph of ΔH vs. the molar ratio of L₀/M₀ sigmoidal (s-shaped) and not hyperbolic? One clue is that the molar ratio of ligand (titrant) to macromolecule centers around one, so, as explained in earlier sections, when L₀ is not >> M₀, the graph will not be hyperbolic. 

Let's use a specific example to illustrate these ideas. A soluble form of the HIV viral membrane protein, gp120 (4 μM), was placed in the calorimetry cell. A form of its natural ligand, CD4, a membrane receptor protein from T helper cells, was placed in the syringe and titrated into the cell (Myszka et al. 2000). Enthalpy changes/injection were determined. The data were transformed and fit to an equation that shows the ΔH "normalized to the number of moles of ligand injected at each step". Figure \(\PageIndex{3}\) shows the raw data (top, μcal/s) for each injection, and the best-fit model (bottom), assuming a 1:1 stoichiometry of CD4 (the "ligand") to gp120 (the "macromolecule"), with a K_D = 190 nM.

Figure \(\PageIndex{3}\): Titration Calorimetry determination of K_D and ΔH for the interaction of gp120 and CD4

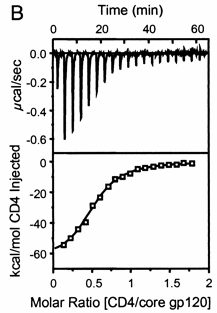
Note that the bottom curve is sigmoidal, not hyperbolic (we'll explain this below). A single experiment can determine the stoichiometry of binding (n), the K_D, and the ΔH₀. From the value of ΔH^o and K_D and the relationship ΔG^o = -RTlnK_eq = RTlnK_D = ΔH₀ - TΔS^₀, the ΔG^₀ and ΔS^₀ values can be calculated. No separation of bound from free is required. Enthalpy changes on binding were calculated to be -62 kcal/mol (260 kJ/mol).

Let's briefly review fractional saturation (Y) plots to review differences in Y vs. L and Y vs. L₀ (total ligand) when L₀ is not >> M₀. Graphs for each are shown below in Figure \(\PageIndex{4}\).

Figure \(\PageIndex{4}\): Y vs L and Y vs L₀ when L₀ is not >> M₀

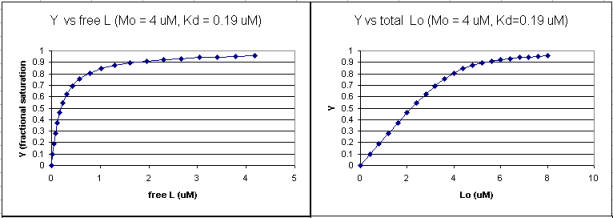
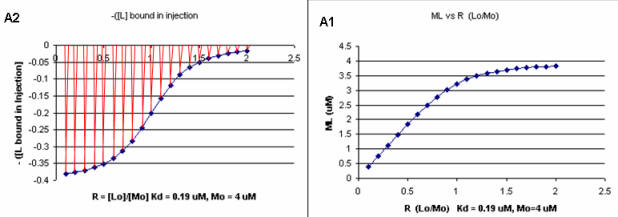
The graph of Y vs L (left) is hyperbolic, but the graph of Y vs Lo, when Lo is not >> Mo, might appear hyperbolic, but it is not.  Why?  Let's draw a few more graphs to explain.

Figure \(\PageIndex{5a}\)  below shows two graphs.  Figure 5 (top) shows a plot of ML vs R (the ratio of [L₀]/[M₀]). This curve appears hyperbolic, but it is not the same shape as the Y vs. L₀ graph shown in Figure 4 (right). Moreover, if the amount of ligand bound at each injection (calculated by subtracting [ML] for injection i+1 from [ML] for injection i) is plotted vs R (= [L₀]/[M₀]), a sigmoidal curve shown in Figure \(\PageIndex{5}\) (bottom) is seen, which resembles the best-fit graph for the experimentally determine enthalpies in Figure \(\PageIndex{3}\). 

Figure \(\PageIndex{5a}\): Binding Curves that show different binding curves for gp120 and CD4.  Note that the bottom graph shows the negative of the amount of ligand bound per injection

Now let's add the relative enthalpy change (μcal/s) for each injection shown as light red bars to mimic the one in Figures 2 and 3 showing the actual titration calorimetry (μcal/s) data.  This is shown in Figure \(\PageIndex{5b}\)

Figure \(\PageIndex{5b}\): Binding Curves that Explain Sigmoidal Titration Calorimetry Data for gp120 and CD4

Now, let's make this graph interactive in Figure \(\PageIndex{5c}\) so you can visualize each incremental titration injection overlaid on the best fit binding curve (determined from the complete ITC experiment).

p>

Figure \(\PageIndex{5c}\):  Interactive graph to visualize each incremental titration injection overlaid on the best fit binding curve determined from the complete ITC experiment. Red bars are used to represent the actual heat changes for injection instead of the sharp drop and exponential return to baseline seen in Figures 2 and 3.

Surface Plasmon Resonance

A newer technique for measuring binding is surface plasmon resonance (SPR), which uses a sensor chip with a 50 nm gold layer on a glass surface. A carbohydrate matrix is then added to the gold surface. A macromolecule that contains a binding site for the ligand is covalently attached to the matrix. The binding site on the macromolecule must not be perturbed significantly. A liquid containing the ligand is passed over the binding surface.

The detection system consists of a light beam that passes through a prism on top of the glass layer. The light is reflected, but another component of the wave, called an evanescent wave, passes into the gold layer, where it can excite the Au electrons. If the correct wavelength and angle are chosen, a resonant wave of excited electrons (plasmon resonance) is produced at the gold surface, decreasing the total intensity of the reflected wave. The angle of the SPR is sensitive to the layers attached to the gold, and binding and dissociation of the ligand are sufficient to change the SPR angle, as seen in Figure \(\PageIndex{6}\).

Figure \(\PageIndex{6}\): Surface plasmon resonance (SPR) system. SPR detects changes in the refractive index near the surface layer of a sensor chip. The sensor surface is gold, with antibodies attached. During the measurement, the chip is irradiated from the bottom with a beam spanning a wide angle range within the total internal reflection range. The SPR angle shifts (from I to II in the diagram) when biomolecular binding events alter the refractive index at the surface. The detector will determine the angle of the intensity decrease. This change in resonant angle can be monitored non-invasively in real time as a plot of the resonance signal (proportional to the mass change) versus time. Song, Chengcheng & Zhang, Shaocun & Huang, He. (2015). Choosing a suitable method for the identification of replication origins in microbial genomes. Frontiers in MICROBIOLOGY. 6. 10.3389/fmicb.2015.01049. DOI: 10.3389/fmicb.2015.01049. License CC BY 4.0

This technique can distinguish between fast and slow binding/dissociation of ligands (as reflected in on and off rates) and can be used to determine K_D values (through measurement of the amount of ligand bound at a given total concentration of ligand or, more indirectly, through the determination of both k_on and k_off.

Binding DB: a database of measured binding affinities, focusing chiefly on the interactions of proteins with drug targets like drugs.

PDBBind-CN: a comprehensive collection of the experimentally measured binding affinity data for all biomolecular complexes deposited in the Protein Data Bank (PDB).

Extreme Binding Affinities

An incredibly tight binding interaction has recently been reported for Cu¹⁺ binding to the CueR protein from E. coli. Cu¹⁺ ions are usually kept at very low cell concentrations to prevent toxicity. Yet some enzymes require Cu. Free copper ions must be present in the cell to bind to appropriate sites on proteins. How are these competing concerns regulated in the cell? The total Cu concentration in E. coli is about 10 μM (10,000 nM), which, given the bacterium's small size, represents about 10,000 copper ions per cell.

Cells have evolved many mechanisms to control and deliver Cu ions. Copper ions can be delivered to target proteins by copper chaperones (analogs of the chaperone proteins that guide protein folding). CueR in E. Coli appears to regulate the copper-induced expression of genes involved in copper biochemistry (including an enzyme that oxidizes Cu¹⁺ to Cu^2+, which is less toxic). One particular gene that is up-regulated is copA. CueR increases the transcription of copA in the presence of Cu, Ag, and Au (coinage metal) ions. Changela et al. developed an in vitro assay to determine the extent of expression of CueR-regulated genes under various ion types and concentrations. In the assay, purified CueR was added to a gene construct containing the copA promoter (a section of DNA immediately upstream of the copA start site where RNA polymerase binds). Initially, they found that transcription was always on, even in the presence of a ligand, glutathione, which binds Cu¹⁺ avidly and should keep free Cu¹⁺ levels very low. They switched to a more tightly binding Cu¹⁺ ligand, cyanide (CN^-), to further reduce free Cu¹⁺ levels.  Extremely high levels of CN^- (millimolar) stopped transcriptional activation, but if additional Cu1+ was added, activation ensued, suggesting that copper binding to the protein was reversible. At 1 mM CN^-, transcription increased with the addition of copper ions up to a TOTAL Cu¹⁺ concentration of 60 μm. Under these conditions, the free Cu¹⁺ concentrations were much lower. Given the range of CN^- concentrations used, half-maximal activation occurred at a TOTAL Cu¹⁺ concentration of 0.7 μM. Similar activation was observed by Ag¹⁺ and Au¹⁺, but not by Zn and Hg ions, showing the specificity for monovalent cations over divalent cations.

Knowing the pKa of HCN, stability constants for Cu¹⁺:CN^- complexes, and CN- concentrations, Changela et al. made a series of solutions buffered in FREE Cu¹⁺ that extended from 10^-18 to 10^-23 M (pH 8.0). (For example, the log of the binding constant β, logβ, for the Cu¹⁺ + 2CN^- ↔ [Cu(CN)₂]^- is 21.7. You solved problems involving linked equilibrium if you have taken analytical chemistry.) The free Cu¹⁺ concentration at half-maximal activation of gene reporter transcription, a measure of the dissociation constant, K_D, was approximately 1 x 10^-21 M (zeptomolar)! Now, assume that the volume of the contents of an E. Coli cell is 1.5 x 10^-15 L. If there were only one Cu¹⁺ ion in the cell, its concentration would be 10-⁹ M. The values suggest that there are no free Cu¹⁺ ions in the cell and that only 1 Cu⁺¹ ion is sufficient to bind CueR and subsequently activate transcription of copA.

It is essential for survival that bacterial cells get the correct metals to metalloproteins. A recent review by Waldron and Robinson illustrates how. The cell has many mechanisms for restricting the binding of specific metals to the right proteins. In addition, the natural order of stability for transition-metal complexes must be considered when understanding metal affinities. That stability is given by the Irving-Williams series shown below (along with Group 2A metal ions). The trend parallels the size of the cation (going from largest to smallest):

Mn²⁺ < Fe²⁺ < Co²⁺ < Ni²⁺ < Cu²⁺ > Zn²⁺ (tightest binding)

• The ability of a protein to change shape upon ligand binding allows it to bind different metals. For example, cyanobacteria have a high demand for copper and manganese. Manganese might bind to a protein, followed by folding, which traps it in the protein. This unstable metal cannot be replaced by copper, which ordinarily out-competes Mn²⁺ for the site.
• Metal transporters help regulate the intracellular concentration of each metal. These metal transporters control metal-sensing systems that regulate gene expression. Once a metal reaches a sufficient concentration to bind, the metal sensors target mRNA to repress specific genes and halt transcription.
• Another enzyme can also be activated to export the metal. Restricting the concentrations of competing metals allows weaker metal-binding sites to be available.
• Metal sensors can also help regulate which proteins some metals bind to, based on what is available. For example, E. coli switches metabolism to minimize the number of iron-requiring proteins expressed when iron is less abundant.
• Metals are supplied by multiple pathways (advantageous if an important protein in one is defective) and are trafficked to the correct protein through many ligand-exchange reactions.
• Certain enzymes bind specific metals, leading to preferential conformational changes. Hence, if a metal comes along that binds more tightly but is not preferred by the enzyme, it will not trigger the enzyme because it binds differently.

Molecular Basis of High Affinity Interactions

What differentiates high and low affinity binding at the molecular level? Do high-affinity interactions have many intramolecular H-bonds, salt bridges, and van der Waals interactions, or are hydrophobic interactions most important? Recently, the crystal structures of various antibody-protein complexes were determined to study the basis of affinity maturation of antibody molecules. It is well known that antibodies elicited upon exposure to a foreign molecule (antigen) are initially of lower affinity than those produced later in the immune response. An incredible number of different antibodies can be generated by antibody-producing B cells through genetic mechanisms (combining different variable regions of antibody genes through splicing, imprecise splicing, and hypermutation of critical nucleotides in the genes encoding the antigen-binding regions of antibodies). Clones of antibody-producing cells with higher affinity are selected by binding and clonal expansion. Investigators studied the crystal structure of 4 different antibodies that bind to the same site (epitope) on the protein antigen lysozyme. Increased affinity was correlated with increased buried apolar surface area, rather than with increased numbers of H bonds or salt bridges. The data for these antibodies are shown below in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Characteristics of Antibody:Hen Egg Lysozyme Complexes (HEL) from Li,Y. et al. Nature: Structural Biology. 6, pg 484 (2003)

Antibody	H26-HEL	H63-HEL	H10-HEL	H8-HEL
KD (nM)	7.14	3.60	0.313	0.200
Intermolecular Interactions
H bonds	24	25	20	23
VDW contacts	159	144	134	153
salt bridges	1	1	1	1
Buried Surface Area
ΔASURF (A2)	1,812	1,825	1,824	1,872
ΔASURF-polar (A2)	1,149	1,101	1,075	1,052
ΔASURF-apolar (A2)	663	724	749	820

Electrostatic interactions between biological molecules remain very important, even though we often consider them nonspecific. Consider the binding of DNA-binding proteins with positive domains to the negative polyanion, DNA. The initial encounter will be electrostatic in origin and important for targeting proteins to DNA, where other specific interactions may occur.

In a similar example (Yeung, T. et al.), it was recently reported that moderately positively charged proteins are directed to endosomes and lysosomes via interactions with the negatively charged membrane phosphatidylserine (PS). In contrast, more positively charged proteins are targeted to the inner surface of the plasma membrane, which is enriched in PS and phosphorylated phosphatidylinositol derivatives (PIP₂, PIP₃), as shown in Figure \(\PageIndex{7}\).

Figure \(\PageIndex{7}\): Negatively charged phospholipids in biological membranes

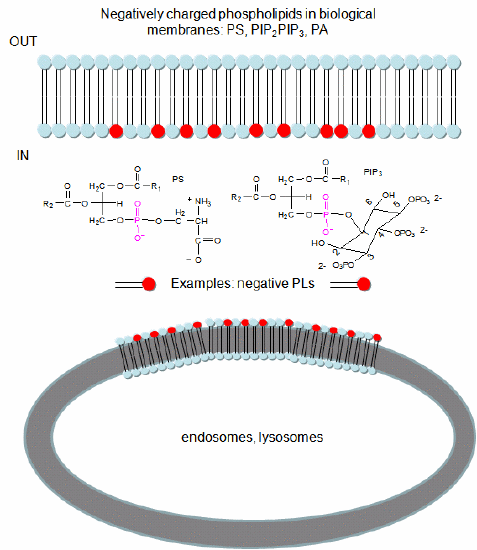
To study this, they used the C2 domain of lactadherin (Lact-C2) from milk that binds PS in the presence of calcium. The C2 domain was covalently linked to the green fluorescent protein. This protein contains an internal fluorophore composed of three amino acids (Ser65-Tyr66-Gly67) that cyclizes spontaneously upon folding to produce a fluorophore that emits green light. A fusion gene encoding Lact-C2 and GFP was introduced into wild-type (WT) and PS-deficient mutant yeast. It is bound to the inner leaflet in WT cells and endosome and lysosome vesicles, but is diffused through the cytoplasm in mutant cells. They also made cationic probes with farnesyl tails that could anchor the soluble probes to membranes. The most positively charged probes were recruited to the plasma membrane inner leaflet, while less charged ones were recruited to internal vesicles. The authors speculate that PS on cytoplasmic membrane layers can target signal transduction proteins to these regions.

Antibodies with Infinite Affinity. Chmura et al. PNAS. 98, pg 8480 (1998)

Docking

The quantitative methods described above do not elucidate the binding mechanism. Computer programs have been developed that allow the docking of a ligand (a small molecule or even another protein) to another protein. Free programs such as Autodock can model the automatic docking of flexible ligands to proteins. Molecular dynamics simulations are used to study the actual binding and unbinding processes.  See Chapter 5.8 for more details on docking programs.

The Crowded Cell

Most binding studies are performed in vitro at dilute concentrations of both the macromolecule and the ligand. Are these conditions illustrative of conditions inside a cell? The answer is no! Cells are crowded with organelles, macromolecular complexes, and cytoskeletal components that provide an internal architecture to the cell. The total macromolecular concentration in the cell has been estimated to be as high as 400 g/L, or 400 g/1000 mL, or 0.4 g/mL, or 400 mg/mL. Try to dissolve a water-soluble protein like albumin at those concentrations! From 5 to 40% of the entire cellular volume is occupied by large molecules, and at the upper range, very little space exists for other large macromolecules. A representation showing the crowdedness of a bacterial cell at the atomic level is shown in Figure \(\PageIndex{8}\).

Figure \(\PageIndex{7}\): (A) Schematic illustration of Mycoplasma genitalium (MG). (B) Equilibrated MG_h system highlighted with proteins, tRNA, GroEL, and ribosomes. (C) MG_h cl ose-up showing atomistic level of detail. Yu et al. (2016) eLife 5:e19274. https://doi.org/10.7554/eLife.19274. Creative Commons Attribution License.

Imagine trying to diffuse through that! 

Summary

(Summary written by Claude, Sonnet 4.6, Anthropic)

This chapter extends the theoretical framework for ligand-macromolecule binding established in the previous section into the experimental domain — describing how K_D values are measured, what molecular features determine binding affinity, and how the highly crowded intracellular environment modifies the binding interactions studied in vitro.

Experimental measurement of K_D requires distinguishing the concentration of the bound complex ML from the concentrations of free M and free L at equilibrium. Methods that require physical separation include gel filtration chromatography (in which the ML complex elutes ahead of free L, with the bound ligand revealed as a transient dip in the free ligand baseline), membrane filtration (in which nitrocellulose or similar membranes irreversibly bind protein, retaining both M and ML while free L passes through), precipitation with ammonium sulfate (which co-precipitates ML), and equilibrium dialysis (in which M is enclosed in a dialysis membrane permeable to small L, and the excess ligand inside the bag at equilibrium represents bound ligand). The critical requirement for separation-based methods is that the equilibrium not be significantly perturbed during separation. Methods that avoid separation are generally preferred: spectroscopic methods (monitoring absorbance or fluorescence changes in either the ligand or the macromolecule upon complex formation), isothermal titration calorimetry (ITC), and surface plasmon resonance (SPR).

ITC is particularly powerful because it is label-free and directly measures thermodynamic quantities. In ITC, a concentrated ligand is injected in small aliquots into a cell containing a macromolecule, and the heat released or absorbed per injection — measured by maintaining an equal temperature between the sample and reference cells through precisely controlled current application — is recorded as a function of the cumulative molar ratio L₀/M₀. The result is a sigmoidal rather than hyperbolic binding curve because (1) the experiment measures the differential heat per injection (the change in ML between successive injections, not the total ML), and (2) the concentrations of M and L are comparable (L₀ is not >> M₀), placing the experiment in the regime where the quadratic binding equation applies and produces the characteristic non-hyperbolic, near-linear-then-plateauing binding profile. Mathematical fitting of the sigmoidal enthalpy curve to a binding model yields K_D, the stoichiometry n, and ΔH° simultaneously; ΔG° = −RT ln(1/K_D) and ΔS° = (ΔH° − ΔG°)/T are then calculated. For the gp120-CD4 interaction, ITC determined K_D = 190 nM and ΔH° = −62 kcal/mol, illustrating the extreme enthalpic favorability of some protein-protein interactions. SPR measures binding in real time by detecting changes in refractive index at a gold sensor surface as ligand flows over an immobilized macromolecule, providing the time-resolved association and dissociation phases of the binding event from which k_on, k_off, and K_D = k_off/k_on are extracted.

Molecular determinants of binding affinity are revealed by comparing the crystal structures and K_D values of four antibodies that bind the same epitope on hen egg-white lysozyme. The result is unambiguous: increasing affinity (from K_D = 7.14 nM to 0.20 nM) correlates with increasing buried apolar surface area (663 to 820 Ų), while the number of hydrogen bonds (~20–25) and salt bridges (invariably 1) remains essentially constant. The hydrophobic effect — the enthalpically unexpected but entropically driven burial of nonpolar surface — is thus the principal thermodynamic contributor to high-affinity protein-ligand interactions at the molecular level, consistent with the small-molecule thermodynamic analysis in earlier chapters. Electrostatic interactions, while often nonspecific, play critical roles in the initial diffusional encounter and in directing proteins to specific cellular compartments: moderately cationic proteins are targeted to endosomes and lysosomes through interactions with negatively charged phosphatidylserine, while more strongly cationic proteins are recruited to the plasma membrane inner leaflet, which is enriched in PS and phosphoinositides.

At the extreme end of the affinity range, the Cu¹⁺-CueR interaction in E. coli illustrates both extraordinary binding tightness and its biological logic. By using CN⁻-buffered metal solutions of known free [Cu¹⁺] (derived from linked equilibria with known stability constants), Changela et al. determined that CueR responds to free Cu¹⁺ concentrations of ~10⁻²¹ M — a zeptomolar K_D meaning that the bacterium's entire copper inventory (~10,000 ions per cell in a volume of ~1.5 × 10⁻¹⁵ L, equivalent to a total concentration of ~10⁻⁸ M) is effectively entirely protein-bound, with no free Cu¹⁺ ions present. A single Cu¹⁺ ion in the cell is sufficient to occupy CueR and activate copA transcription. This extreme affinity is part of a sophisticated cellular metal homeostasis system that uses the Irving-Williams stability series, metal chaperones (analogous to protein-folding chaperones), metal transporters, metal sensors that regulate gene expression, restricted access to binding sites through conformational gating, and enzyme-catalyzed metal export — all coordinated to deliver the correct metal to the correct protein while excluding competing metals.

Finally, the chapter emphasizes that virtually all binding measurements are conducted in dilute aqueous solutions that bear little resemblance to the actual intracellular environment. Cells are extraordinarily crowded: total macromolecular concentrations of 400 mg/mL mean that 5–40% of cellular volume is physically occupied by large molecules, restricting diffusion, dramatically altering effective concentrations through excluded-volume effects, and potentially shifting binding equilibria substantially relative to dilute in vitro measurements. A realistic understanding of protein-ligand interactions in vivo requires accounting for these crowding effects — an active area of research that remains incompletely understood.