4.1: Main Chain Conformations
- Page ID
- 14934
Search Fundamentals of Biochemistry
Introduction
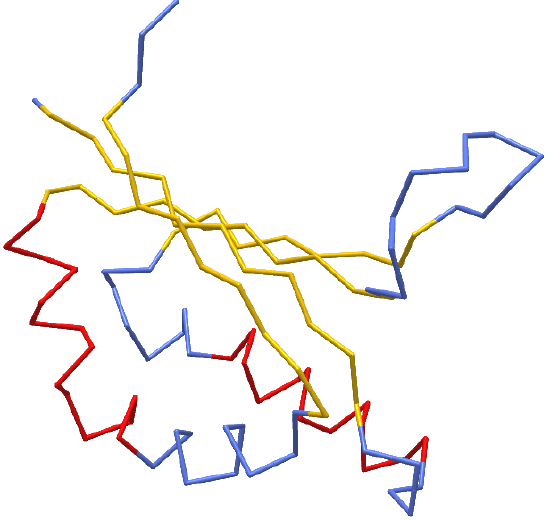
In Chapter section 3.2, we discussed primary, secondary, tertiary, and quaternary structures of proteins. We used as an example the protein hydroxynitrile lyase (5Y02). An interactive iCn3D model of hydroxynitrile lyase is shown in Figure \(\PageIndex{1}\).
Figure \(\PageIndex{1}\): hydroxynitrile lyase (5Y02). Click the image for a popup or use this external link:
https://structure.ncbi.nlm.nih.gov/icn3d/share.html?gGY8QBkCP8dPmfoH6 (Copyright; author via source)
Blue indicates random coil, red indicates alpha helices and yellow shows beta strands. As we discussed in Chapter 3.2, the beta strand backbones are quite extended compared to the alpha helices which are more compressed. Atomic force microscopy can be used to pull the helix into alternative extended shapes. Let's explore main chain conformations in greater detail.
If we wish to understand protein structure, it is important to first understand the possible conformations of the backbone chain before we start considering the effect of side chains and the overall structure of the protein. Where do we start? It's a very complicated topic but we can simplify it by considering the structures of short hydrocarbons and other organic groups and use ideas you learned in earlier chemistry courses. So let's start with butane, a 4C hydrocarbon.
You will remember from previous chemistry courses that different rotational conformations (conformers) of butane have different energies. These conformers are often visualized using Newman projections sighting down the internal C2-C3 carbon bond in butane. The figure below shows ball and stick representations as well as Newman projects for three different conformers formed by rotation around the C2-C3 bond. You are familiar with bond angles, which is the angle between two bonds connecting three connected atoms. For this discussion, we will consider the dihedral angle which describes the angle of rotation around the middle bond of a 4-atom, 3-bond connected system. It's easiest to use Newman projections to understand dihedrals, which represents the angle between groups bonded to the front and back (circle) atoms sighted down the front-to-back atoms. Figure \(\PageIndex{2}\) shows multiple conformers of butane, represented in ball and stick form or as Newman projections.
The syn and eclipsed conformer with a dihedral angle of 0° has the highest energy since the two eclipsed bonds have high torsional energy and the two closest approaching H atoms on the methyl C atoms have steric (1,6) interactions. Rotating the front C 60° gives a gauche conformation of lower energy. Rotating to 120° leads to higher energy given the torsional strain between the eclipsed bonds. Rotating fully to 180° gives the conformer of lowest energy and torsional (bond-bond) strain. Steric strain between the two closest H atoms on the methyl groups also raises the energy.
A red line has been drawn between the 4 carbon atoms connected by three bonds in the anti or trans-conformer. Notice that the red line is a zig-zag as shown in the rotated red line drawing beneath the ball and stick conformer shown. All the conformers are available but the anti or trans-confomer is most stable and abundant.
Now, let's try this approach on a more complicated molecule, a 12-carbon atom carboxylic acid, dodecanoic acid. Figure \(\PageIndex{3}\) shows the molecule in the all- trans conformation (where all the carbon atoms in the chain are arranged in an anti, zig-zag manner), and a second gauche conformation for the bond highlighted by a red line. Note that rotation around that bond to produce the gauche conformer, a higher energy form, produces a kink in the chain. We will see this again when we discuss lipid structure.
Now let's compare the all-trans dodecanoic acid structure to one largely extended conformer of a tetrapeptide, Gly-Gly-Ala-Gly (GGAG) as shown in Figure \(\PageIndex{4}\).
Notice the similarities in these two structures. The atoms in the main chain of the peptide, N, Ca, C (the carbonyl C) are arranged in the familiar zig-zag fashion, characteristic of the lowest energy conformer. The dihedral angles along the backbone would be, to a first approximation, around + 180° depending on whether the rotation is clockwise or counterclockwise from the syn conformer. However, the actual conformation of the GGAG peptide, if found as part of the primary structure of a protein, could adopt a whole range of other conformers with potentially different dihedral angles for each bond in the main chain. Look back at the iCn3D model for hydroxynitrile lyase above and it should be clear that if the stretch of amino acids Gly-Gly-Ala-Gly is in a beta sheet, its dihedral angles for the main chain would be closer to +1800 than if they were in an alpha helix, which would dihedral angles much less than 180°, perhaps closer to + 600
It might seem like all possible dihedral angles are possible for the main chain atoms of a protein, which would make understanding protein structure too complicated for our minds to comprehend. However, that are two major things that simplify conformational analyzes of proteins.
Trans and Cis Peptide Bonds
Note in the extended peptide example in the above figure, the alpha Cs of adjacent amino acids are on opposite sides of the peptide bond between the carbonyl carbon atom and the amide nitrogen atom. They are trans to that bond. A rectangle was drawn on the above figure centered on the C-N peptide bond for two adjacent amino acids to clearly show the trans orientation of the alpha Cs.
Rotation around single bonds can occur, so an isomerization of the trans peptide bond to the cis isomer can occur. Both isomeric forms of the dipeptide Ala-Ala are shown in the top part of Figure \(\PageIndex{5}\).
This trans arrangement of the alpha Cs in Ala-Ala and most internal X-Y amino acids pairs in a protein is sterically favored by a factor of 1000/1 over the cis form, which clearly shows torsional between the aligned (red) bonds and steric strain between amino acid side chain atoms.
The case is different for X-Y amino acid pairs when Y is proline, which is shown in the bottom part of the above figure. Proline is a cyclic amino acid and as such would be expected to be more sterically restricted in a protein sequence. In X-Pro peptide bonds in proteins, the trans/cis ratio is about 4/1. Clearly the torsional (between bonds) and steric strain (between atoms) are similar in both isomers.. You would expect to find both trans and cis X-Pro peptide bonds in proteins given the constraints placed on protein conformation in the tertiary structure of the protein.
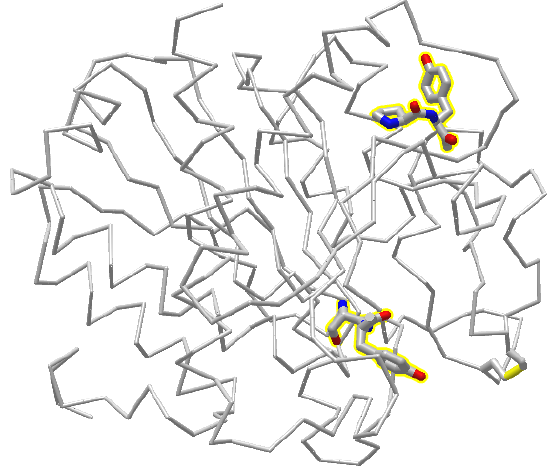
Figure \(\PageIndex{6}\) is an interactive iCn3D model showing two pairs of X-Y peptide bonds in the protein carboxypeptidase. Answer the questions below about the two pairs of peptide bonds, which are shown in stick form and CPK colors.
Figure \(\PageIndex{6}\): 2 peptide bonds in carboxypeptidase. Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...3ARF97MgN4427A (Copyright; author via source)
Exercise \(\PageIndex{1}\)
Two X-Y amino acids are shown in stick form in the protein carboxypeptidase A
1. What is the sequence of each pair shown from N to C terminus
2. Are the X-Y peptides bonds cis or pro?
- Answer
-
Add texts here. Do not delete this text first.
Backbone dihedral angles and Ramachandran Plots
Now let's focus on possible dihedral angles for the peptide bond in protein chains. Just as saturated fatty acid chains have preferred conformations (all anti or trans), peptide chains also have preferred conformations. The complexity is much greater, however. For our example using dodecanoic acid, we dealt only with torsion or dihedral angles around the methylene (-CH2-) carbons. For proteins, we must consider the covalent links which attach the amino acids together, as well as the rotations possible in 20 different amino acids. The peptide bond connects the carbonyl C of the ith amino acid to the alpha amine N of the i th+1 amino acid. The resulting bond is an amide link. X-ray analysis shows that the C-N bond has double bond character. This can be accounted for by delocalizing the nonbonding electron pair of the N to the carbonyl C forming a double bond, with the pi-bonded electrons of the carbonyl C-O bond moving to the O. These resonance structures lead to a planar arrangement of the peptide carbonyl C and amide N and the two other atoms connected to each, since the hybridization of the C and N has sp2 character, with 120o bond angles, as illustrated in Figure \(\PageIndex{7}\).
Figure \(\PageIndex{7}\): Resonance forms of peptide bond
This greatly simplifies the number of conformations that a protein can adopt since these 6 atoms can be considered to reside and move in a plane. The alpha C serves as the corner attachment point of two different planes, each of which can rotate independently of the other plane. The two planes can twist around the alpha carbon. The rotation angles for the two planes are called phi (φ) and psi (ψ) are analogous to the torsion angles in the acyl chain of dodecanoic acid. They can vary from -180 to +180o. The R group substituent attached to the alpha C can also rotate around the alpha C and the beta C of the side chain. This angle is defined as chi. Other rotations also occur within the side chain. We will concentrate on phi (φ) and psi(ψ) angles.
Figure \(\PageIndex{8}\) shows the peptide Gly-Gly-Ala-Gly (at high pH to give the protonation state shown) with the six atoms around the C-N peptide bonds shown in rectangles. Phi (φ) and psi (ψ) angles are also shown.
Using these ideas, we can consider a protein backbone as a series of linked sequences of rigid, planar peptide units which can rotate around phi/psi angles. When the chain is fully extended (as shown in the links above), φ/ψ are + 180o, with the syn eclipse form defined as having 00 φ/ψ angles. When φ and ψ equal 0o, the two peptide bonds flanking the alpha Cs are in the same plane. This conformation is prohibited since the O of the C=O on one plane and the H of the H-N on the other are overlapping - i.e. they approach closer than their van der Waals radii.
The Proteopedia site below gives a phenomenal explanation and visual representation of φ/ψ angles in proteins.
 Proteopedia: Ramachandran principle and phi psi angles
Proteopedia: Ramachandran principle and phi psi angles

Ramachandran was the first to calculate which φ/ψi angles are allowed. He modeled the angles permitted to a tripeptide, assuming the atoms were hard spheres. The angles allowed depended in part on the limiting distance chosen for interatomic contacts. (i.e. the usual H -- H distance is 2.0 angstroms, and 3.0 for C--C bonds.) The plot below shows the allowed regions in red. Only 3 small regions of conformational space are available. If you allow a closer approach by 0.1 angstroms, more conformation space is available, but only one new area is available, shown in yellow in Figure \(\PageIndex{10}\).
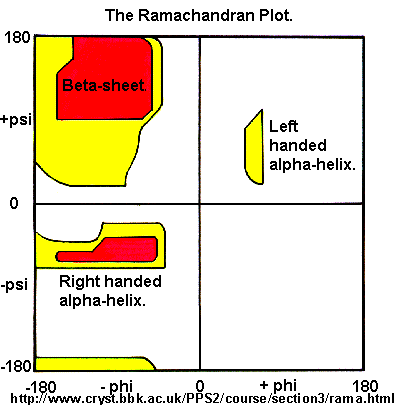
Right-hand alpha helices fall at -570,-470 while left hand alpha helices fall at +570,+470. (Notice these are not mirror images of each other. The mirror image of a right-handed alpha helix would be a left-handed helix made of D-amino acids.) Parallel beta sheets are at -1190, -1130, while antiparallel sheets falls at -1390, +1350. Note that beta sheets have φ/ψ angles closer to the fully extended + 1800 of the all anti (trans) conformation of dodecanoic acid than does the alpha helix which is more compact. Other types of helices also are found. The 310 helix, a sharper helix with 3 amino acids/turn, falls at -490,-260. All of these examples of secondary structure fall in allowed regions.
Modern Ramachandran plots do not model the atoms as hard spheres but instead consider the potential energy of the atoms using the Lennard-Jones potential (6-12 potential) for induced dipole-induced dipole interactions. We discussed this potential function Chapter 2.4.
A Ramachandran plot of Ala-Ala-Ala is nearly identical to the plot for Phe-Phe-Phe (which is unbranched at the beta carbon, the first methylene C in the side chain). The plot for Thr-Thr-Thr, which has a branch at the beta C (with OH and CH3 attached) shows somewhat less room than the other plots. Pro-Pro-Pro is most restricted for obvious reasons.
For a longer chain than a tripeptide, there are more restrictions than for (Ala)3, since the chain can't assume a conformation when it passes through itself. The plots for actual proteins have many points which do fall in forbidden regions. However, these points would be allowed if the peptide bonds twist a few degrees. Gly bonds also fall outside the allowed regions. This is understandable, since the side chain of Gly is H, and it is used in proteins where sharp turns of the chain are necessary.
Figure \(\PageIndex{11}\) shows Ramachandran plots for Gly, Ala, Tyr, and Pro in actual proteins (made years OK but can't find reference)
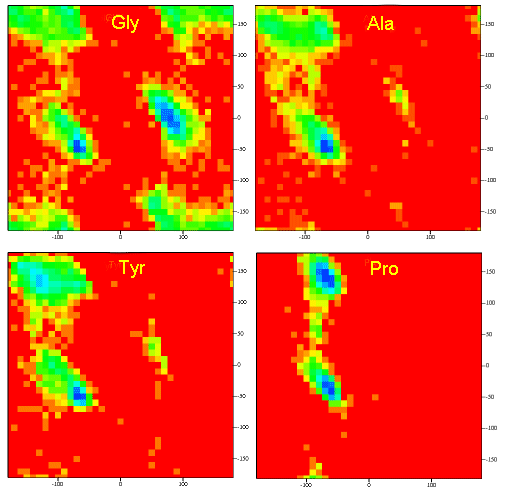
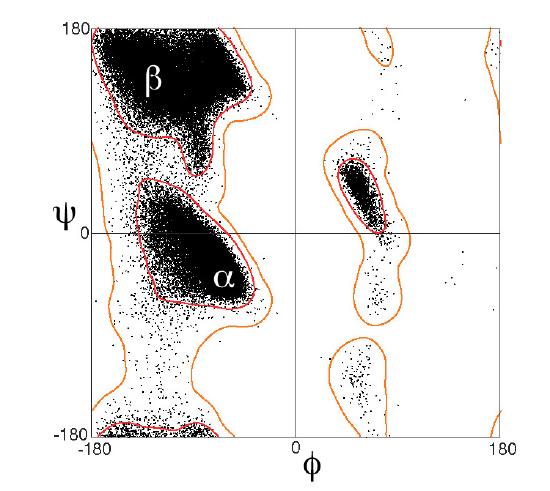
Figure \(\PageIndex{12}\), taken from the Proteopedia page above, shows the Ramachandran plots for 100,000 proteins from the Protein Data Bank.
Now it's time to explore in more detail secondary, tertiary and quaternary structures in more detail. There are many ways to organize the structural organization of the protein world. For the rest of this chapter, we will adopt the approach used by Carl Branden and John Tooze in their seminal book, "Introduction to Protein Structure".