B1. Binding of a Single Ligand
- Page ID
- 4912
The following derivations and graphs are derived from the equation for fractional saturation \(Y = [L]/(K_d + [L])\). Assume that the error in Y is +/- 0.02 at each [L] for the following analysis. Likewise, consider a constant error in L
Hyperbolic Fits
For the equilibrium:
\[ M + L \rightleftharpoons ML,\]
with
\[ [ML] = \dfrac{[M_o][L]}{K_d+ [L]} \]
or expressed in terms of fractional saturation (Y)
\[ Y = \dfrac{[L]}{K_d+ [L]}.\]
A plot of \(Y\) vs. \(L\) gives a hyperbola, as shown in the figure below.
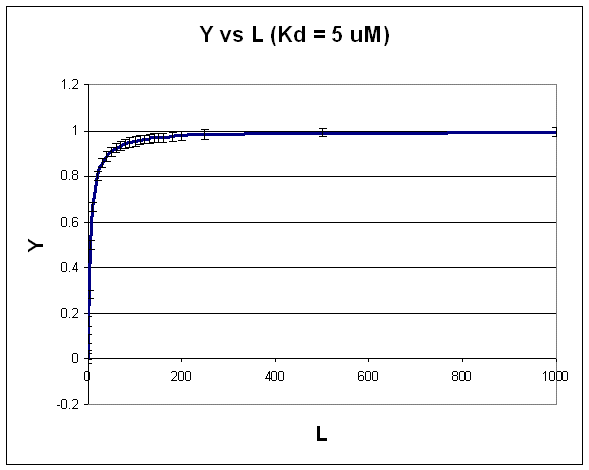
Figure: Hyperbola
Note that the constant error bars are shown on the diagram as well. Remember, you can not easily determine the Kd from a hyperbolic fit (Kd = L at half saturation) unless you have truly reached saturation. A better way to determine Kd from hyperbolic binding data is to actually fit all the data to an equation for a hyperbola using a non-linear regression program, such as found in Mathcad. Remember, however, bad data can still be fit.
![]() Mathcad 8 - Nonlinear Hyperbolic Fit. A: Mo and Kd | B: Kd
Mathcad 8 - Nonlinear Hyperbolic Fit. A: Mo and Kd | B: Kd
DOUBLE-RECIPROCAL PLOT: FIT TO LINEAR REGRESSION EQUATION.
\[ \dfrac{1}{Y} = \dfrac{K_d + L}{L} = \dfrac{K_d}{L} + 1\]
This double-reciprocal plot is the form \(y = mx + b\), where \(y = 1/Y\), m = \(K_d\), x = 1/L, and \(b = 1\).
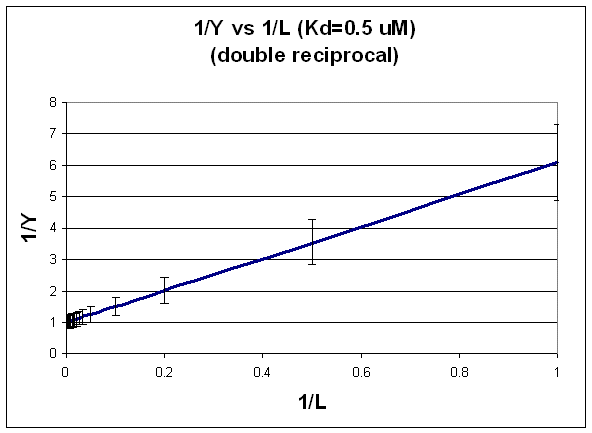
Figure: double-reciprocal plot
Notice in this that the errors are not constant. This is easily shown by the following example.
- If Y = 1 +/- 0.02 (as in the above examples), then Y could vary from 0.98 - 1.02 (range of 0.04). 1/Y would vary from 1/1.02 - 1/0.98 or 0.98 - 1.02. (range of 0.04)
- If, Y = 0.1 +/- 0.02, then Y could vary from 0.08 -0.12, a range again of 0.04. But now, 1/Y would vary from 1/0.12 - 1/0.08, or 8.33 - 12.5, (range of 4.17! Notice that as Y is smaller, I/Y get bigger and the error "envelope" gets larger.
You can not legitimately use linear regression analysis on the straight line double reciprocal plot, since the error at each point is not constant. You can use LR analysis to determine the slope if you can weight each point differently. Clearly in this case, the higher Y or lower 1/Y values would be weighted more. Given the availability of computer programs for fitting non-linear equations, the linear double-reciprocal plot is not used often to extract the best value of Kd. However, it is very useful in getting an estimate of Kd which can then be used in a non-linear fit as described in A. In addition, it still has widespread use in the visual analysis of multiple binding curves in the absence and presence of different concentrations of an inhibitor of binding. We will see this use later when we study enzyme kinetics.
Scatchard Plots
\[ \frac{Y}{K_d + L} = L \]
or
\[ \dfrac{Y}{K_d}+ YL = L \]
or
\[ Y\,K_d = L - YL = L (1 - Y) \]
which gives
\[ \dfrac{Y}{L} = \dfrac{1-Y}{K_d} = \dfrac{-Y}{K_d} + \dfrac{1}{K_d}\]
This equation, known as the Scatchard equation, is of the form \(y = mx + b\),
with
- \(y = \dfrac{Y}{L}\),
- \(x = Y\),
- \(m = \dfrac{-1}{K_d}\), and
- \(b = \dfrac{1}{K_d}\).
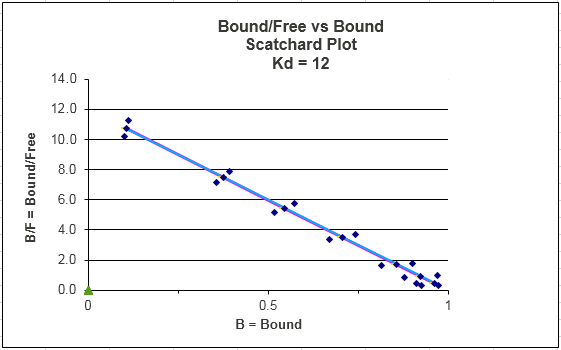
Figure: Scatchard Equation
If we assume as above there is error in Y (or bound B term) and not L, then both axes must have error attributable to the Y term. The following description of error analysis in Scatchard plots and the graph above was kindly contributed by George Dombi at the University of Rhode Island. "The only concentration that has a vertical error bar is the zero free concentration. The error bars should run on a line that emanates from the origin through the plotted point itself (blue dots in the above graph). This line gets more and more horizontal at higher levels of free Ligand. This is what makes using the Scatchard plot a problem when trying to dissect two or more single binding lines from the data visually." This fitting method is one of the most misused.
Notice that Y/L appears to go to 0/0 when L approaches 0. This actual limiting value can be determined from l'Hopital's rule: the limiting ratio is given by the limit of the derivative of the numerator (Y) divided by the derivative of the denominator (L). This value is 1/Kd.
Curvilinear Scatchard plots are often observed. These can result from several reasons, including:
- a mixture of two different M's, with different Kd's
- M binding more than 1 ligands with different Kd's
- M binding more than 1 ligand in which binding of the first decreases the Kd for the second (positive cooperativity) or vice-versa (negative cooperativity).
SEMI-LOG PLOT:
The best way to visualize whether saturation is reached is by plotting Y vs log L since the plot rises steeply and plateaus quickly compared to the hyperbolic plot which plateaus slowly.
Figure: Y vs log L
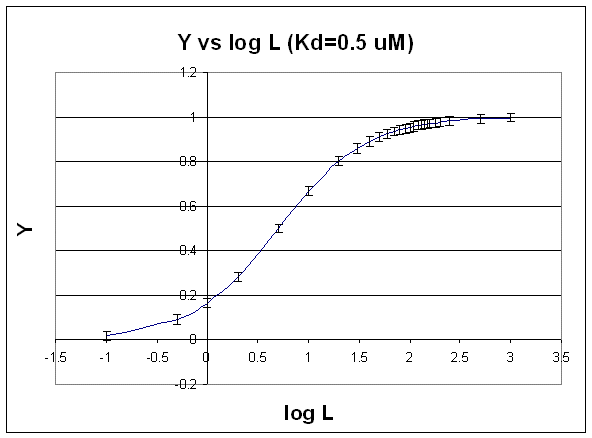
Second, it is logical to plot Y vs log L since the extent of binding is determined by the chemical potential of L and M, and the chemical potential of L is proportional to log L. Even if you get a good non-linear fit to a hyperbola (as in A above), you should do a Y vs log L plot to see how close to saturation you have come.
We can think about the nature of the Y vs log L plot by comparing it to the results we derived using the Henderson-Hasselbach equation. From that equation, we could calculate, given a pH, the protonation state of an acid. We determined that if the pH was 2 units below the pKa, the ratio of [HA]/[A-] = 100/1 or about 100% of the acid was protonated. Likewise, if the pH was 2 units above the pKa, the ratio of [HA]/[A-] = 1/100 or about 100% of the acid was deprotonated. If the pH = pKa, 50% of the acid was protonated. In this example we really looked at fractional saturation of the acid (i.e. how much was bound to protons) as a function of the log L where L was [H3O+].
Now lets apply this to the equilibrium \(M + L \rightleftharpoons ML\). We wish to know how much is bound, or the fractional saturation, as a function of the log L. Consider three examples.
- L = 0.01 \(K_d\)(i.e. L << Kd), which implies that \(K_d\)= 100L. Then Y = L/[Kd+L] = L/[100L + L] ≈1/100. This implies that irrespective of the actual [L], if L = 0.01 \(K_d\), then Y ≈0.01.
- L = 100 \(K_d\)(i.e. L >> Kd), which implies that \(K_d\)= L/100. Then Y = L/[Kd+L] = L/[(L/100) + L] = 100L/101L ≈ 1. This implies that irrespective of the actual [L], if L = 100 \(K_d\), then Y ≈1.
- L = \(K_d\), then Y = 0.5
These scenarios show that if L varies over 4 orders of magnitude (0.01Kd < \(K_d\) < 100Kd), or, in log terms, from -2 + log \(K_d\)< log \(K_d\)< 2 + log Kd), irrespective of the magnitude of the \(K_d\), that Y varies from approximately 0 - 1. In other words, Y varies from 0-1 when L varies from log \(K_d\) by +2. Hence, plots of Y vs log L for a series of binding reactions of increasingly higher \(K_d\)(lower affinity) would reveal a series of identical sigmoidal curves shifted progressively to the right. This is shown in the figure below.
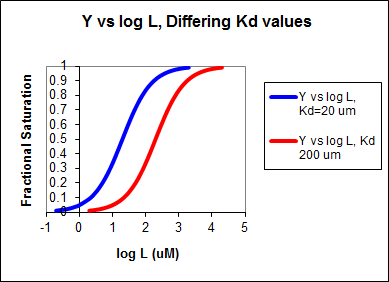
Figure: Y vs Log L, Differing Kd values
 Wolfram Mathematica CDF Player - Interactive Graph of Y vs log L at different Kd values (free plugin required)
Wolfram Mathematica CDF Player - Interactive Graph of Y vs log L at different Kd values (free plugin required)
NOTE: I have derived equations and plots above using the variables Y and L. Remember, Y = ML/Mo. I could easily substitute ML/Mo is all of the above equations, and get plots using ML and L. Mo, a constant, would then be factored into the slope and intercept terms.


