A3. Dimerization and Multiple Binding Sites
- Page ID
- 4906
In the previous examples, we considered the case of a macromolecule M binding a ligand L at a single site, as described in the equation below:
\[M + L \rightleftharpoons ML \]
where
\[K_d = \dfrac{[M][L]}{[ML]}. \label{1}\]
We saw that the binding curves (\(ML\) vs. \(L\) or \(Y\) vs. \(L\) are hyperbolic, with a \(K_d = L\) at half maximal binding.
A special, yet common example of this equilibrium occurs when a macromolecule binds itself to form a dimer, as shown below:
\[ M + M \rightleftharpoons M^2 = D \]
where \(D\) is the dimer, and where
\[K_d = \dfrac{[M][M]}{[D]} = \dfrac{[M]^2}{[D]} \label{11} \]
At first glance you would expect a graph of \([D]\) vs. \([M]\) to be hyperbolic, with the \(K_d\) again equaling the \([M]\) at half-maximal dimer concentration. This turns out to be true, but a simple derivation is in order since in the previous derivation, it was assumed that \(M_o\) was fixed and \(L_o\) varied. In the case of dimer formation, \(M_o\), which superficially represents both \(M\) and \(L\) in the earlier derived expression, are both changing.
One again a mass balance expression for \(M_o\) can be written:
\[[M_o] = [M] + 2[D] \label{12}\]
where the coefficient 2 is necessary since their are 2 M in each dimer.
More generally, for the case of formation of trimers (Tri), tetramers (Tetra), and other oligomers,
\[ [M_o] = [M] + 2[D] + 3[Tri] + 4[Tetra] + \: .... \label{13} \]
Rearranging Equation \ref{12} and solving for \(M\) gives
\[[M] = [M_o] -2[D] \label{14}\]
Substituting Equation \ref{14} into the \(K_d\) expression (Equation \ref{1}) gives
\[K_d = \dfrac{(M_o-2D)(M_o-2D)}{D} \]
where can be rearranged into quadratic form:
\[4D2 - (4M_o+K_d)D + (M_o)^2 = 0 \label{15} \]
which is of the form \(y = ax^2+bx+c\). Solving the quadratic equation gives \([D]\) at any given \([M_o]\). A value \(Y\), similar to fractional saturation, can be calculated, where \(Y\) is the fraction of total possible \(D\), which can vary from 0-1.
\[Y = \dfrac{2[D]}{[M_o]} \label{16}\]
A graph of \(Y\) vs \(M_o\) with a dimerization dissociation constant \(K_d = 25\, \mu M\), is shown below.
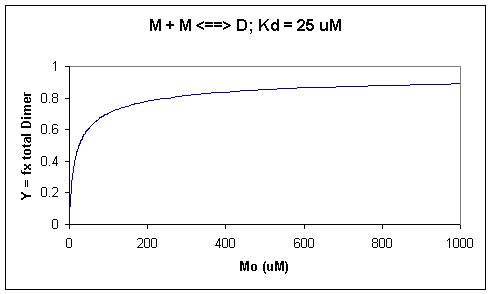
Figure 1: Saturation binding curve for dimerization of a macromolecule
Note that the curve appears hyperbolic with half-maximal dimer formation occurring at a total \(M\) concentration \(M_o = K_d\). Also note, however, that even at \(M_o = 1000 \,\mu M\), which is 40x \(K_d\), only 90% of the total possible \(D\) is formed (\(Y = 0.90\)). For the simple
\[M + L <=> ML\]
equilibrium, if \(L_o\) = 40x the \(K_d\) and \(M_o \ll L_o\), then
\[ Y = \dfrac{L}{K_d+L} = \dfrac{L}{(L/40)+L} = 0.976 \]
The aggregation state of a protein monomer is closely linked with its biological activity. For proteins that can form dimers, some are active in the monomeric state, while others are active as a dimer. High concentrations, such as found under conditions when protein are crystallized for x-ray structure analysis, can drive proteins into the dimeric state, which may lead to the false conclusion that the active protein is a dimer. Determination of the actual physiological concentration of \([M_o]\) and \(K_d\) gives investigators knowledge of the \(Y\) value which can be correlated with biological activity. For example, interleukin 8, a chemokine which binds certain immune cells, exists as a dimer in x-ray and NMR structural determinations, but as a monomer at physiological concentrations. Hence the monomer, not the dimer, binds its receptors on immune cells. Viral proteases (herpes viral protease, HIV protease) are active in dimeric form, in which the active site is formed at the dimer interface.
Another Special Case: Binding of L to 2 sites with different Kds
Check out the interactive graph to see how the relative sizes of the Kds affect it.
 Wolfram Mathematica CDF Player - Binding of L to 2 Sites (free plugin required)
Wolfram Mathematica CDF Player - Binding of L to 2 Sites (free plugin required)


