D1: Introduction to Chemical Potential
- Page ID
- 4684
We have studied the intermolecular forces involved when single chain amphiphiles and double chain amphiphiles form micelles and bilayers, respectively. To gain a greater insight into the these processes, we need to understand the thermodynamics of micelle and bilayer formation. First we must understand the concept of chemical potential, which is related to the free energy of a reaction.
\(\Delta G\), the free energy change for a reaction, determines the spontaneity and extent of a chemical or physical reaction. The free energy of system depends on 3 variables, T, P, and n, the number of moles of each substance. If the system is composed of two different parts, \(A\) and \(B\), the system is at equilibrium (ΔG=0) if Ta = Tb, Pa = Pb, and dG/dn for A (μa) equals μb. \(μ\) is the chemical potential of a substance, where \(μ_a\) is given as
\[μ=μ^o +RT\ln [A].\]
The chemical potential is really the free energy per mole.
Expressed in more formal mathematical terms, since the natural variables of G and μ are T, P, and n, we can write:
\[dG = (ƒG/ƒT)_{P,n} + (ƒG/ƒP)_{T,n} + (ƒG/ƒn)_{P,T}\]
where (ƒG/ƒx)y,z is the derivative (partial) of \(G\) with respect to \(x\) at constant \(y\) and \(z\). That is the total \(dG\) consist of contributions to the change of \(G\) from changes in T, P and n.
Since \(G\) and \(\mu\) are quite similar, the following series of analogous equations apply:
\[ΔG = ΔG^o + RT \ln Q_{rx}\]
is analagous to
\[Δμ = Δμ^o + RT\ln Q_{rx}\]
where \Q_{rx}\) is the
\[\text{reaction quotient} = \dfrac{[P][Q]}{[A][B]}\]
for the reaction
\[A+B \rightleftharpoons P+Q \]
\(ΔG = ΔH - TΔS\) is analogous to
\[Δμ =ΔH - TΔS\]
\[ΔG^o = ΔH^o - T ΔS^o\]
is analogous to \(Δμ^o = ΔH^o - TΔS^o\)
\[ΔG^o = - RT\ln K_{eq}\]
is analogous to
\[Δμ^o = - RT\ln K_{eq}\]
Thermodynamics of Micelle and Bilayer Formation
First, let's consider the thermodynamics of micelle formation, based on the equation below:
\[n \,SCA <==> 1\, micelle\]
where SCA represents a single chain amphiphile. At first glance we might suspect that:
- ΔHo < 0 since the van der Waals interactions among the buried acyl chains in the micelle would be much more favorable than the water - acyl chain interactions for the monomeric amphiphile in solution. This notion is supported by our aphorism, "like dissolves like". Of course, we couldn't ignore polar interactions (H bonding for example) among the head groups and water, but we might expect these to be equally favorable in both the monomeric and micellular states.
- ΔSo < 0 since we are forming a state (a single micelle) with much less positional entropy from a state (single chains amphiphiles dispersed in solution) with much more positional entropy.
Hence it would appear that micelle formation is enthalpically favored, but entropically disfavored. Lets examine this issue more closely. First we need to obtain a greater understanding of Δμo which should give us a clue as to where a SCA would "want" to be in this mixture. Remember, Δμo depends only on the relative stability of a molecule in a given environment and not its concentration.
Traube, in 1891, noticed that single chain amphiphiles tend to migrate to the surface of water and decrease its surface tension (ST.) He observed that the decrease in ST is directly proportional to the amount of amphiphile, added up until a certain point, at which added amphiphile has no additional effect. In other words, the response of ST saturates at some point.
We are more interested in what happens to amphiphiles in bulk water, not at the surface. As we mentioned earlier, monomeric single chain amphiphiles are in equilibrium with single chain amphiphiles in micelles. Assume you have a way to measure monomeric single chain amphiphile in solution. What happens to its concentration as you add more and more SCA to the mixture? Turns out you observe the same effect that Traube noted with changes in surface tension. This explanation goes like this: as more amphiphile is added, more goes into bulk solution as monomers. At some point, there are enough amphiphiles added to form micelles. After this point, added amphiphiles forms more micelles and no further increases in monomeric single chain amphiphile are noted. The concentration of amphiphile at which this occurs is the critical micelle concentration (CMC).
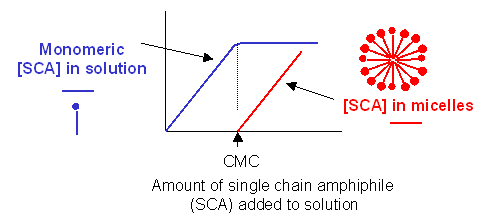
Figure: Graph showings distribution of single chain amphiphiles in bulk aqueous solution
This saturation effect can be observed with other systems as well.
- measure the amount of NaCl(aq) in solution as more NaCl(s) is added to water. At some point, the water is saturated with dissolved NaCl, and no further increase in NaCl (aq) occurs.
- measure the amount of a sparing soluble hydrocarbon (HC) into water. After saturation, phase separation occurs.
Consider the example of adding a great excess of NaCl(s) to water. At the very time the salt is added, the system is clearly not in equilibrium. Therefore, Δμ< 0. Write the reaction as follows:
NaCl(s) ------------> NaCl (aq).
Let x stand for NaCl. Therefore,
\[Δμ = μ_x\,(aq) - μ_x\,(s) = μ^o_x(aq) + RT \ln x\,(aq) - \left(μ^o_x\,(s) + RT \ln x\,(s)\right)\]\]
In this equation, all terms are constant except RT ln x(aq), since all the Δμo values are constant, independent of concentration. Remember, RTln x(s) is constant since the concentration of a solid is constant. With time, Δμ becomes less negative, until the system reaches equilibrium, and Δμ = 0. The term RT ln x(aq) becomes more positive since the x(aq) is increasing. When μ x(aq) = μ x(s), no further NaCl dissolves. Remember, a condition for equilibrium is μa = μb.
Now consider the addition of a drop of a slightly soluble hydrocarbon (HC) into water, as pictured in the diagram below. At t=0, the system is not at equilibrium and some of the HC will transfer from the pure liquid to water, so at time t=0, \(Δμ < 0\).
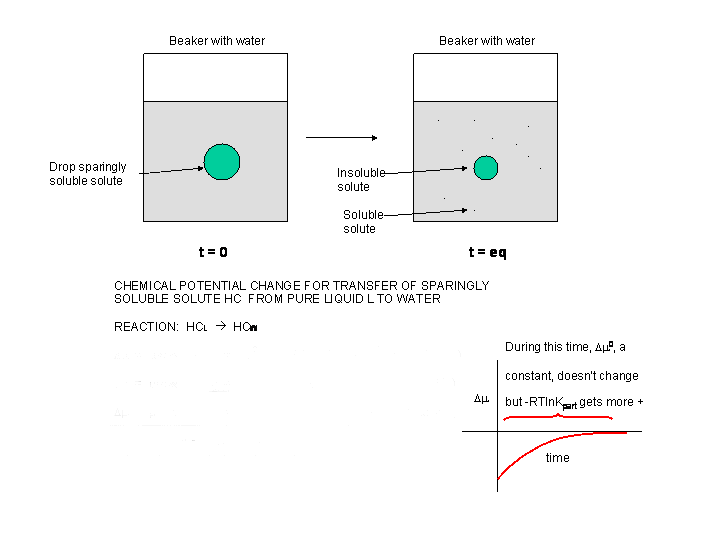
Figure: \(Δμ\) for transfer of a sparingly soluble liquid solute into water
Δμ = μ HC-W - μ HC-L = μo HC-W + RT ln [HC-W] - (μo HC-L + RT ln [HC-L] =
Δμ = μ HC-W - μ HC-L = (μo HC-W - μo HC-L) + RT ln [HC-W - RT ln HC-L) =
Δμ= Δμo + RT ln (HC-W/HC-L)
Now add a bit more complexity to the last example. Add a hydrocarbon x, to a biphasic system of water and octanol. At t = 0, the system is not at equilibrium. A simple favorable reaction can be written for this system x aq -------> x oct. Clearly, Δμ < 0. Also, Δμo < 0, since this term is independent of concentration and depends only on the intrinsic stability of x in water in comparison to that of octanol. The following equation holds as well:
Δμ = μ x(oct) - μ x(aq) = μo x(oct) + RT ln x(oct) - (μo x(aq) + RT ln x(aq)) =
Δμ= (μo x(oct) - μo x(aq) ) + RT ln (x(oct)/x(aq)) =
Δμ = Δμo + RT ln (x(oct)/x(aq))
Most of the time, we will be interested in Δμo , which depends only on the relative stability, in this case, of x in octanol vs water. Clearly, in this case, Δμo < 0. At equilibrium Δμ = 0. By setting the last equation equal to 0, we can see that
\[Δμ^o = - RT \ln \left (\dfrac {x(oct)}{x(aq)} \right)\]
where the concentration are equilibrium concentrations. We can rewrite this equation as
\[Δμ^o = - RT \ln K_{eq}\]
where Keq is the equilibrium partition coefficient for X in octanol and water. This can readily be determined in the lab. Just shake a separatory flask with a biphasic system of octanol and water after injecting a bit of X. Then separate the layers and determine the concentration of x in each phase. Plug these numbers into the last equation. Remember, you should be able to predict the sign and relative magnitude of Δμo since it does not depend on concentration, but only on the intrinsic stability of the molecules in the different environments.


