D. Bonded Interaction Energy
- Page ID
- 4668
The mathematical form of the energy terms varies from force-field to force-field. The more common forms will be described.
Stretching Energy: \(\mathrm{E_{stretch} = \sum_{bonds}k_b (r - r_o)^2}\)
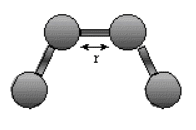
The stretching energy equation is based on Hook's law. The kb parameter defines the stiffness of the bond spring. R0 is the equilibrium distance between the two atoms. It should make sense that deviations from the equilibrium length would be associated with higher energy. The E vs r curves is hence a parabola:
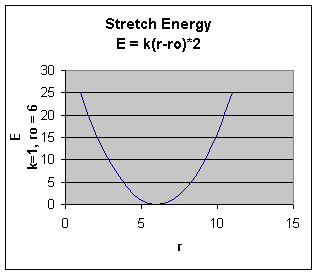
Obviously only small changes in r are allowed as to large an r value would lead to bond breaking.
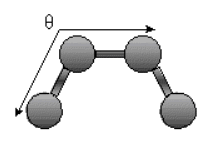
Bending Energy: \(\mathrm{E_{bending} = \sum_{angles} k_Θ (Θ - Θ_o)^2 }\)
 .
.
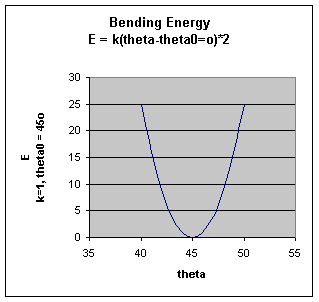
The bending energy equation is also based on Hook's law. The kΘ parameter controls the stiffness of the angle spring, while the Θ0 is the equilibrium angle. As above, the graph of E vs theta is expected to be a parabola.
.
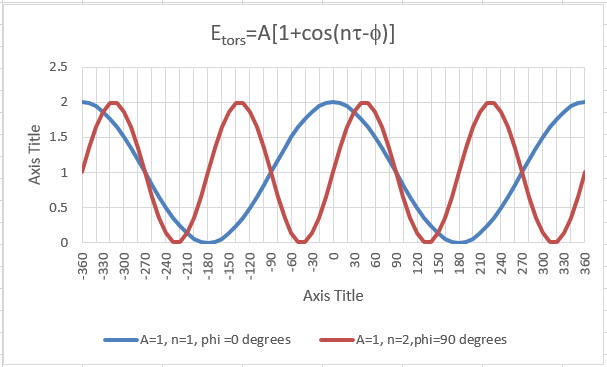
Torsion Energy \(\mathrm{E_{torsion} = \sum_{torsions} A [1 + \cos ( ntau - Θ) ] }\)
The torsion energy is modeled by a periodic function, much as you have seen with energy plots associated with Newman projections sighting down C-C bonds for butane, for example.
 Wolfram Mathematica CDF Player - Torsional Energy (free plugin required)
Wolfram Mathematica CDF Player - Torsional Energy (free plugin required)
The parameters (determined for different 4 bonded atoms small molecules using curve fitting) for these are:
- amplitude A
- periodicity n (ethane, sighting along the C-C axis in a Newman projects displays a periodicity of 120 degrees)
- phase shift Phi: shifts curve along rotation (tau) axis. parameter controls its periodicity, and phi shifts the entire curve along the rotation angle axis (tau).


