B1: Single Step Reactions
- Page ID
- 5070
We will first explore the kinetics of non-catalyzed reactions as we did with our study of passive and facilitated diffusion. Before we do that, a brief review of the two major types of kinetic equations that you studied in general chemistry is in order. You learned two methods to analyze kinetic data:
- initial velocity method: In this method, the initial rate, \(v_0\), is measured as a function of the concentration of reactants. The initial velocity, \(v_0\), is the initial slope of a graph of the concentration of reactants or products as a function of time, taken over a range of times such that only a small fraction of A has reacted. Under these condition, [A] over this short range of time is approximately constant and equal to Ao. Initial rate graphs are often based on measurement of product increase with time (dP/dt) so v0 vs A plots have positive slopes. The velocity at time t along the A vs t curve, dA/dt, is constantly changing as [A] decreases since the velocity depend on the [A]. To reiterate, the initial velocity of the reaction is the slope of the initial linear part of the decay curve when the rate is essentially linear over a narrow range of A concentrations.
- integrated rate method: In this method a differential equation which gives the change of A or P with time (dA/dt or dP/dt) is integrated to give a rate equation giving the concentration of A or P as a function of time. .
REVIEW OF ELEMENTARY REACTION KINETICS
First Order Reaction:
\[ A \xrightarrow{k_1} P \]
where k1 is the first order rate constant. For these reactions, the velocity of the reaction, \(v\), is directly proportional to [A], or
\[ v = \dfrac{-d[A]}{dt} = \dfrac{+d[P]}{dT} = k_1[A] \label{1a} \]
The negative sign in \(-d[A]/dt\) indicates that the concentration of \(A\) decreases. The equation could also be written as:
\[ v = \dfrac{-d[A]}{dt} = -k_1[A] \label{1b}\]
For the rest of the reactions shown in this chapter, I will follow the convention of writing all velocities expressed as \(d[x]/dt\) as positive numbers. A negative sign for a term on the right hand side of the differential equation (as in 1b) will indicate that the concentration dependency of that term will lead to an decrease in \([x]\) with time. Likewise a positive sign for the term on the right hand side of the equation will indicate that concentration dependency of that term will lead to an increase in \([x]\) with time.
Using this nomenclature, the following separable differential equation can be written and solved to find \([A]\) as \(A\) function of \(t\).
\[ \dfrac{d[A]}{dt} = -k_1A \]
\[ \int _{[A_o]}^{[A]} \dfrac{d[A]}{dt} = -k_1[A] \]
evaluate this integral at the limits assuming \( t_0 = 0 \)
\[ ln\; [A] - ln\; [A_o] = - k_1t - 0\]
\[ ln\; [A] = ln\; [A_o] - k_1t \]
or
\[ [A] = [A_o] e^{- k_1t} \label{2} \]
which is characteristic of first-order kinetics.
Equation \ref{2} is an example of an integrated rate equation. The following graphs show plots of \(A\) vs. \(t\) and \(\ln\,A\) vs. \(t\) for data from \(A\) first order process. Note that the derivative (\(\frac{dA}{dt}\)) of the graph of \(A\) vs. \(t\) is the velocity of the reaction. The graph of \(\ln\, A\) vs. \(t\) is linear with \(A\) slope of \(-k_1\).The velocity of the reaction (slope of the \(A\) vs. \(t\) curve) decreases with decreasing \(A\), which is consistent with equation 1. Again, the initial velocity is determined from data taken in the first part of the decay curve when the rate is linear and little \(A\) has reacted (i.e., \([A] \approx [A_0]\)).
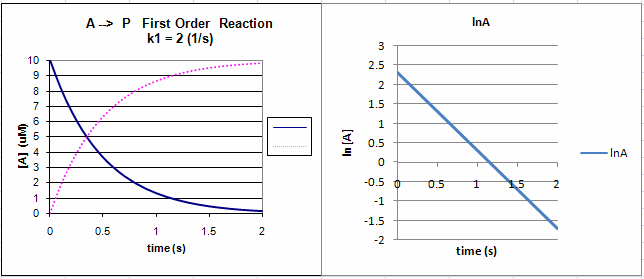
Figure 1: First Order Reaction: \( A \rightarrow P\)
Once again, for complete clarification, another way of analyzing the kinetics of \(A\) reaction, in addition to following the concentration of \(A\) reactant or product as \(A\) function of time and fitting the data to an integrated rate equation, is to plot the initial velocity, \(v_o\), of the reaction as \(A\) function of concentration of reactants. The initial velocity is the initial slope of \(A\) graph of the concentration of reactants or products as \(A\) function of time, taken over \(A\) range of times such that only \(A\) small fraction of \(A\) has reacted, so \([A]\) is approximately constant = \(A_o\). From the first order graph of \(A\) vs. \(t\) above, the slope approaches 0 with increasing time as \([A]\) approaches 0, which clearly indicates that the reaction velocity depends on \(A\). For \(A\) first order process, two equivalent equations, 1a and 1b, can be written.
- Equation 1a above is written showing the disappearance of A as \[v = -\dfrac{d[A]}{dt} = k_1[A]\], while
- Equation 1b above is written showing the appearance of A as \[v = \dfrac{d[A]}{dt} = -k_1[A].\]
Both equations shows that v is directly proportional to A. As [A] is doubled, the initial velocity is doubled.
Velocity graphs used by biochemists often show the initial velocity of product formation (not reactant decrease) as a function of reactant concentration. Hence, as the concentration of product is increasing, the slopes of initial velocity are positive. A graph of v (= dP/dt) vs [A] for a first order process would have a positive slope and be interpreted as showing that the rate of appearance of P depends linearly on [A].
Second Order/Pseudo First Order Reactions
There are two general types of second-order reactions depending on the character of the reacting species. The first type involves two different species (\(A\) and \(B\)) reacting:
\[ A +B \xrightarrow{k_2} P \]
with \(k_2\) as the second-order rate constant. For this irreversible reactions, the rate (velocity) of the reaction, \(v\), is directly proportional to \([A]\) and \([B]\):
\[ v = \dfrac{d[A]}{dt} = \dfrac{d[B]}{dt} = -k_2[A][B] \label{3a}\]
For the second type of second order reaction involves two identical species (\(A\) and \(A\)) reacting:
\[ A +A \xrightarrow{k_2} P \]
or
\[ 2A \xrightarrow{k_2} P \]
also with \(k_2\) as the second-order rate constant.
For this irreversible reactions, the rate (also known as velocity) of the reaction, (\(v\)), is directly proportional to \([A]\) and \([B]\):
\[ v = \dfrac{d[A]}{dt} = -k_2[A][A] = -k_2[A]^2 \label{3b} \]
We will consider two special cases of this reaction type.
Case 1: Pseudo-First Order Kinetics
\([B] \ll [A]\). Under these conditions, \([B]\) never changes, so Equation \ref{3} becomes
\[ v = -(k_2[B]) [A] = -k_1' [A] \label{4}\]
where \(k_1'\) is the pseudo first order rate constant (= \(k_2[B]\) ) for the reaction. The reaction appears to be first order, depending only on [A].
Case 2: Second Order Kinetics
The only reactant is \(A\) which must collide with another \(A\) to form \(P\), as illustrated in the second reaction above. The derivations below apply to this special case.
The following differential equation can be written and solved to find \([A]\) as a function of \(t\).
\[ v = \dfrac{d[A]}{dt} = +2\dfrac{d[P]}{dT} = -k_2[A][A] = - k_2[A]^2 \label{5} \]
\[\dfrac{dA}{dt}=-k_2A^2\]
\[ \int_{A_o}^A \dfrac{dA}{A^2} = \int_{A_o}^A A^{-2}\,dA = -k_2 \int_0^t dt\]
\[ \left.\dfrac{A^{n+1}}{n+1} \right|_{A_o}^A = \left.\dfrac{A^{-1}}{-1}\right|_{A_o}^A =\left. -k_2\,t \right|_0^t \]
\[ -\dfrac{1}{A}-\left(-\dfrac{1}{A_0}\right)= -k_2\,t\]
\[ \dfrac{1}{A} = \dfrac{1}{A_o}+k_2t \label{6}\]
The following graphs show plots of \(A\) vs. \(t\) and \(1/A\) vs. \(t\) for data from a second order process.
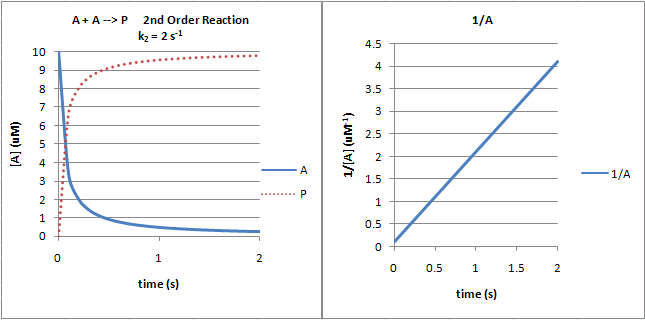
Figure 2: Second Order Reaction: \(A + A \rightarrow P\)
Note that just from a plot of \(A\) vs. \(t\), it would be difficult to distinguish a first from second order reaction. If the plots were superimposed, you would observe that at the same concentration of \(A\) (10 for example as in the linked plots), the \(v_o\) of a first order reaction would be proportional to 10 but for a second order reaction to 102 or 100. Therefore, the second order reaction is faster (assuming similarity in the relative magnitude of the rate constants) as indicated by the steeper negative slope of the curve. However, at low \(A\) (0.1 example), the \(v_o\) of a first order reaction would be proportional to 0.1 but for a second order reaction to 0.12 or 0.01. Therefore, the second order reaction is slower.
The interactive graphs below show the first and second order conversion of reactant \(A\) to product. Change the slides to see how the curves are different.
![]() 4/26/13
4/26/13 Wolfram Mathematica CDF Player - Comparision of 1st and 2nd Order Conversion of A --> P (First order - solid line; Second order - dashed line) (free plugin required)
Wolfram Mathematica CDF Player - Comparision of 1st and 2nd Order Conversion of A --> P (First order - solid line; Second order - dashed line) (free plugin required)


